▷ Derivada de una resta (fórmula y ejercicios resueltos)

En este post te explicamos cómo derivar una resta de funciones (fórmula). También encontrarás ejemplos de derivadas de restas y ejercicios resueltos paso a paso para practicar.

Índice

Fórmula de la derivada de una resta

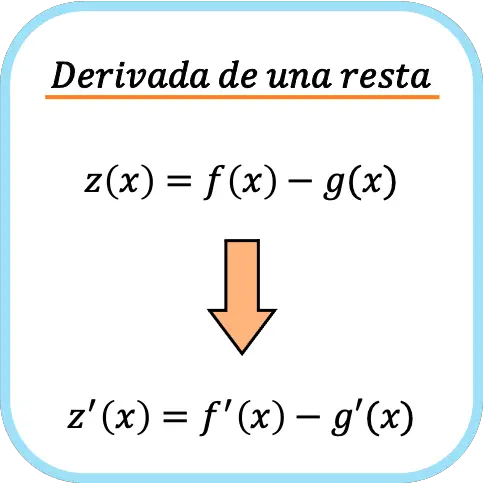
La derivada de una resta de dos funciones es igual a la resta de la derivada de cada función por separado.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

Es decir, derivar dos funciones por separado y luego restarlas es equivalente a primero restar las funciones y luego hacer la derivada.

Asimismo, se aplica la misma regla de derivación para restas de dos o más funciones, por lo que si tenemos una resta de tres, cuatro, cinco,… funciones debemos derivar cada una por separado y luego restarlas.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

Como puedes comprobar, la fórmula de la derivada de una diferencia de funciones es muy parecida a la regla de la derivada de una suma.

➤ Ver: derivada de una suma de funciones

Ejemplos de la derivada de una resta

Una vez hemos visto cuál es la fórmula de la derivada de una resta, ahora pasamos a analizar varios ejemplos de derivadas de este tipo de operaciones para entender del todo cómo se derivan las restas de funciones.

Ejemplo 1: Derivada de una resta de funciones potenciales

$f(x)=x^3-4x$

La derivada de la resta de dos funciones es equivalente a la diferencia de la derivada de cada función por separado. Así que primero calcularemos la derivada de cada función por separado:

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

Por lo tanto, la derivada de toda la función es la siguiente:

$f'(x)=3x^2-4$

Ejemplo 2: Derivada de una resta de funciones distintas

$f(x)=\text{cos}(x)-\log_7(x^2)$

Para derivar la resta de funciones, primero debemos derivar las dos funciones por separado y luego restarlas.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

Y después de hacer las dos derivadas, las restamos con el mismo orden original:

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

Ejemplo 3: Derivada de una resta al cuadrado

$f(x)=\left(x^7-2x^3-9\right)^2$

En este caso tenemos una función compuesta, porque se trata de una resta entre tres funciones elevada al cuadrado. De modo que debemos emplear la fórmula de la derivada de una función potencial y la regla de la cadena para calcular la derivada de toda la función:

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤ Ver: fórmula de la derivada de una potencia

Ejercicios resueltos de la derivada de una resta

Deriva las siguientes restas de funciones:

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

Ver solución

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

Demostración de la derivada de una resta

A continuación, demostraremos la fórmula de la derivada de una resta de funciones partiendo de la definición de la derivada, que es:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Entonces, si z es la diferencia de dos funciones diferentes:

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

Sustituimos z por la resta de las funciones en la expresión del límite:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

Ahora haremos una transformación para así separar la fracción y obtener una resta de dos fracciones:

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

Aplicando las leyes de los límites, podemos separar la expresión anterior en dos límites diferentes. Porque el límite de una resta es igual a la resta de los límites:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Si nos fijamos, cada límite corresponde a la derivada de una función, lo que significa que se cumple la fórmula de la derivada de una diferencia:

$\displaystyle z'(x)=f'(x)-g'(x)$