En este post aprenderás a cómo estudiar la derivabilidad de una función, es decir, saber si una función es derivable o no. Además, veremos la relación que tiene la derivabilidad y la continuidad de una función. Y, finalmente, estudiaremos la derivabilidad de una función a trozos.
Índice
Derivabilidad y continuidad de una función
La continuidad y la derivabilidad de una función en un punto se relacionan de la siguiente manera:
- Si una función es derivable en un punto, la función es continua en ese punto.
- Si una función no es continua en un punto, tampoco es derivable en ese punto.
Sin embargo, el recíproco de este teorema es falso, es decir, que una función sea continua en un punto no significa que siempre sea derivable en ese punto.
También se puede ver si una función es derivable o no en un punto a partir de su representación gráfica:
- Si es un punto suave la función es derivable en ese punto.
- Si es un punto anguloso la función es continua pero no derivable en ese punto.
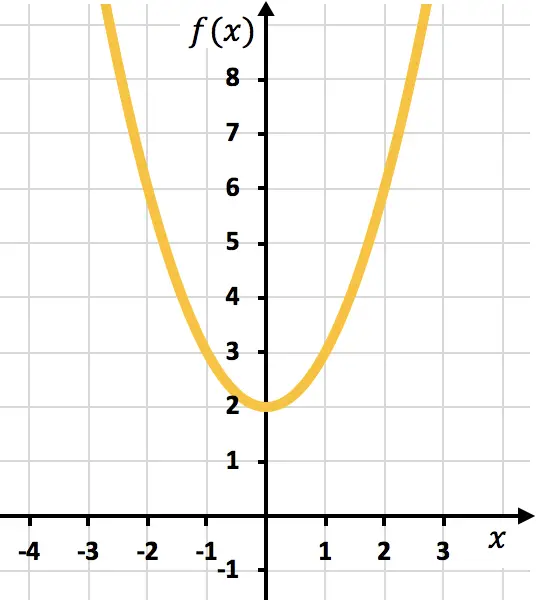
Punto suave en x=0:
función continua y derivable en ese punto.
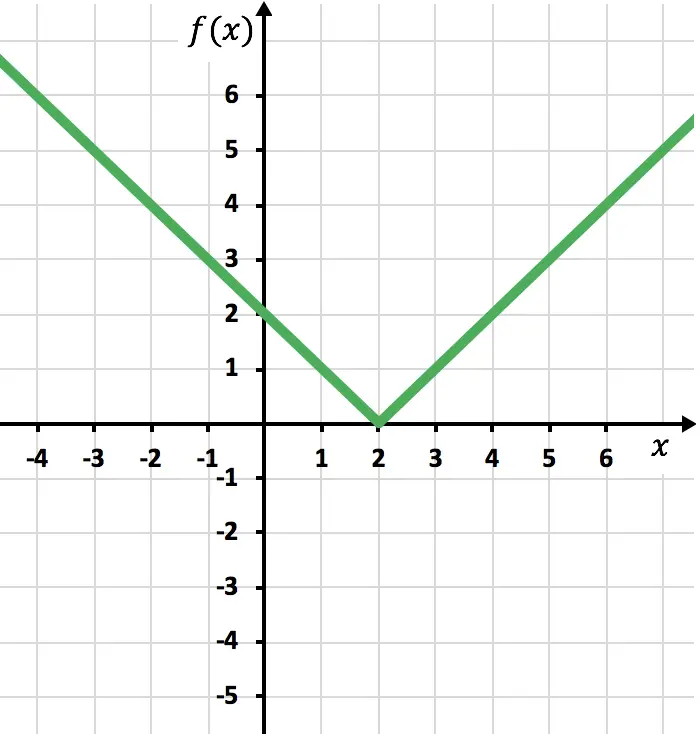
Punto anguloso en x=2:
función continua pero no derivable en ese punto.
Derivabilidad de una función a trozos
Una vez sabemos la relación entre la continuidad y la derivabilidad de una función, vamos a ver cómo estudiar la derivabilidad de una función definida a trozos.
Se puede saber si una función definida a trozos es derivable en un punto calculando las derivadas laterales en ese punto:
- Si las derivadas laterales en un punto no son iguales, la función no es derivable en ese punto:
No es derivable en
- Si las derivadas laterales en un punto coinciden, la función es derivable en ese punto:
Sí es derivable en
Nota: para que una función sea derivable en un punto, la función debe ser continua en ese punto. Por lo tanto, antes de calcular las derivadas laterales debemos asegurarnos de que la función es continua en ese punto. Si no tienes claro cómo se estudia la continuidad en un punto, puedes ver cómo se hace en el siguiente enlace:
Veamos ahora un ejemplo de cómo calcular la derivada de una función definida a trozos en un punto:
- Estudia la continuidad y la derivabilidad de la siguiente función definida a trozos en el punto x=2:
Las funciones de los dos trozos son continuas en sus respectivos intervalos, sin embargo, debemos mirar si la función es continua en el punto crítico x=2. Para ello, resolvemos los límites laterales de la función en el punto:
Los límites laterales en el punto crítico nos han dado el mismo resultado, por tanto, la función es continua en el punto x=2.
Una vez sabemos que la función es continua en x=2, vamos a estudiar la derivabilidad de la función en ese punto. Para ello, calculamos las derivadas laterales de la función definida a trozos:
Ahora evaluamos cada derivada lateral en el punto crítico:
Las dos derivadas laterales nos han dado el mismo resultado, por tanto, la función es derivable en x=2 y el valor de la derivada es 6:
Por otro lado, si las derivadas laterales nos hubiesen dado un resultado diferente, significaría que la función no es derivable en x=2. Es decir, que la derivada en este punto no existiría.
Para terminar, solo comentarte que este procedimiento también es válido para estudiar la derivabilidad de una función con valor absoluto, ya que las funciones con valores absolutos también se pueden definir a trozos. Puedes consultar cómo convertir una función de valor absoluto a trozos aquí:
➤ Ver: cómo definir a trozos una función con valor absoluto
Ejercicios resueltos de la derivabilidad de una función
Ejercicio 1
Estudia la continuidad y la derivabilidad de la siguiente función definida a trozos:
Las funciones de los dos trozos son continuas, pero debemos mirar si la función es continua en el punto crítico x=1. Para ello resolvemos los límites laterales de la función en el punto:
Los dos límites laterales en el punto crítico dan el mismo resultado, por tanto, la función es continua en x=1.
Una vez sabemos que la función es continua en el punto crítico, vamos a estudiar si es derivable en el mismo punto. Así que calculamos las derivadas laterales:
Y evaluamos las dos derivadas laterales en x=1;
Las derivadas laterales no coinciden en el punto x=1 de modo que la función no es derivable en este punto.
Ejercicio 2
Analiza la derivabilidad y la continuidad de la siguiente función definida a tramos:
Las funciones de los dos tramos son continuas en sus intervalos, pero también tenemos que averiguar si la función es continua en el punto crítico de cambio de definición x=1. Así que hacemos los límites laterales de la función en dicho punto:
Los dos límites laterales en el punto crítico dan el mismo resultado, por tanto, la función es continua en x=1.
Y ahora estudiamos si la función es derivable en el punto calculando las derivadas laterales:
Evaluamos las dos derivadas laterales en x=1:
Las derivadas laterales son iguales, de forma que la función es derivable en x=1 y el valor del derivada es 1.
Ejercicio 3
Determina si la siguiente función definida a trozos es continua y derivable en todo su dominio:
Las funciones de los tres trozos son continuas, pero aún debemos verificar si la función es continua en los puntos críticos. Así que primero comprobamos la continuidad de la función en el punto x=-1 resolviendo los límites laterales en este punto:
Los dos límites laterales en el punto x=-1 dan el mismo resultado, por lo que la función es continua en x=-1.
Ahora vamos a comprobar si la función es continua o no en el punto x=2:
Por contra, los límites laterales en el punto x=2 no dan el mismo resultado, así que la función no es continua en x=2. Además, como no es continua en este punto, tampoco será derivable en x=2.
Una vez hemos estudiado la continuidad de la función, pasamos a la derivabilidad. Así que calculamos las derivadas laterales:
Ya sabemos que la función no es derivable en x=2, de modo que solo tenemos que estudiar si la función es derivable en x=-1. Para ello, evaluamos las dos derivadas laterales en el punto:
Las derivadas laterales no coinciden en el punto x=-1, de manera que la función no es derivable en este punto.
Ejercicio 4
Calcula el valor de los parámetros a y b para que la siguiente función definida a trozos sea continua y derivable en todo su dominio:
Independientemente de los valores de las incógnitas, la función es continua y derivable en todos los puntos excepto en x=3, donde debemos comprobar su continuidad y su derivabilidad.
Para que la función sea continua en un punto los dos límites laterales en ese punto deben coincidir. Por tanto, evaluamos los límites laterales en el punto crítico:
De manera que los dos valores obtenidos de los límites laterales deberían ser iguales para que la función sea continua:
Ahora vamos a analizar la derivabilidad en el punto x=3. Hallamos las derivadas laterales:
Y evaluamos las dos derivadas laterales en el punto crítico:
Por tanto, para que la función sea derivable en x=3 los valores obtenidos de las derivadas laterales deberían ser iguales:
Y solucionando esta ecuación podemos hallar el valor de b:
Finalmente, una vez sabemos el valor del parámetro b, podemos calcular el valor del parámetro a resolviendo la ecuación que hemos obtenido antes en los límites laterales:
