▷ Funciones con Valor Absoluto

En esta página se explica qué es una función con valor absoluto. También encontrarás cómo se define una función con valor absoluto a trozos y cómo se representa este tipo de funciones en una gráfica. Además, lo verás con ejemplos de funciones con valor absoluto y podrás practicar con ejercicios y problemas resueltos paso a paso.

Índice

¿Qué son las funciones con valor absoluto?

La definición de una función con valor absoluto es la siguiente:

El valor absoluto de una función convierte todas sus imágenes en positivas. Por lo tanto, el recorrido de una función con valor absoluto nunca puede tener valores negativos.

La siguiente función es un ejemplo de función con valor absoluto:

$f(x)=\lvert 5x \rvert$

Si al evaluar la función en un punto obtenemos un resultado positivo, este se mantiene positivo:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Por contra, si el resultado es negativo se transforma en positivo:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Las funciones con valor absoluto se suelen dar en bachillerato, ya que sus características hacen que sea un poco difícil de entender.

Cómo definir a trozos una función con valor absoluto

Una función con valor absoluto se puede expresar en forma de función definida a trozos (o por partes). Para ello, debemos cambiar de signo a la función en los intervalos que es negativa.

Veamos un ejemplo de cómo pasar de una función con valor absoluto a una función definida a trozos:

Expresa en forma de función definida a trozos la siguiente función con valor absoluto:

$f(x) = \lvert 4 - x^2 \rvert$

Lo primero que debemos hacer es mirar cuándo la función es negativa. Para ello, igualamos a 0 la expresión algebraica de dentro del valor absoluto y resolvemos la ecuación:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Ahora representamos los valores obtenidos en la recta:

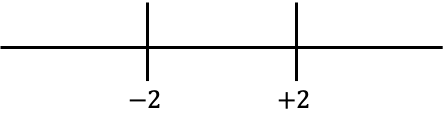
Y miramos qué signo tiene la función sin el valor absoluto en cada intervalo de la recta:

$x<-2$

Cogemos cualquier punto menor que -2, por ejemplo $x=-3:$

$4-(-3)^2$

$-5$

Negativo

$-2 < x < 2$

Cogemos cualquier punto entre -2 y +2, por ejemplo $x=0:$

$4-0^2$

$+4$

Positivo

$x>2$

Cogemos cualquier punto mayor que 2, por ejemplo $x=3:$

$4-3^2$

$-5$

Negativo

Com hemos visto, la función sin el valor absoluto sería negativa en los intervalos $x<-2$ y $x>2.$ Por lo tanto, tenemos que expresar la función a trazos cambiándola de signo en esos intervalos:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.$

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.$

Fíjate que en algún intervalo debes incluir el igual. Por ejemplo, aquí lo hemos puesto en el segundo intervalo $-2 \le x \le 2$ . Pero puedes ponerlo en el intervalo que quieras mientras haya un igual en todos los puntos críticos. Es decir, sería lo mismo si hubiésemos definido la función de la siguiente manera:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Cómo representar una función con valor absoluto

Para representar una función con valor absoluto en una gráfica tenemos que seguir los pasos descritos a continuación:

Representar la función como si no tuviera el valor absoluto.
En los intervalos en los que la función sea negativa, es decir que esté por debajo del eje X, dibujar la función simétrica.
Borrar la parte de la función que queda por debajo del eje X.

Veamos un ejemplo de cómo graficar una función con valor absoluto

Representa gráficamente la siguiente función con valor absoluto:

$f(x) = \lvert -x+2 \rvert$

Para representar una función de valor absoluto primero debemos representar la función sin el valor absoluto. Así que hacemos la tabla de valores de la función sin el valor absoluto:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

Representamos los puntos en un gráfico y trazamos la recta como si fuera una función normal:

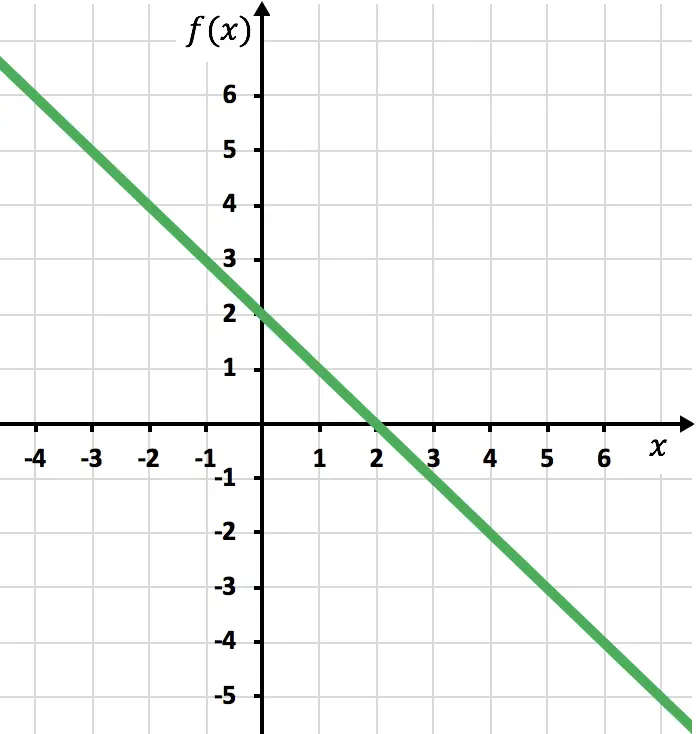
Ahora tenemos que dibujar la función simétrica donde la función sea negativa, es decir, donde esté por debajo del eje de las abscisas. Por tanto, invertimos la función a partir de x=2:

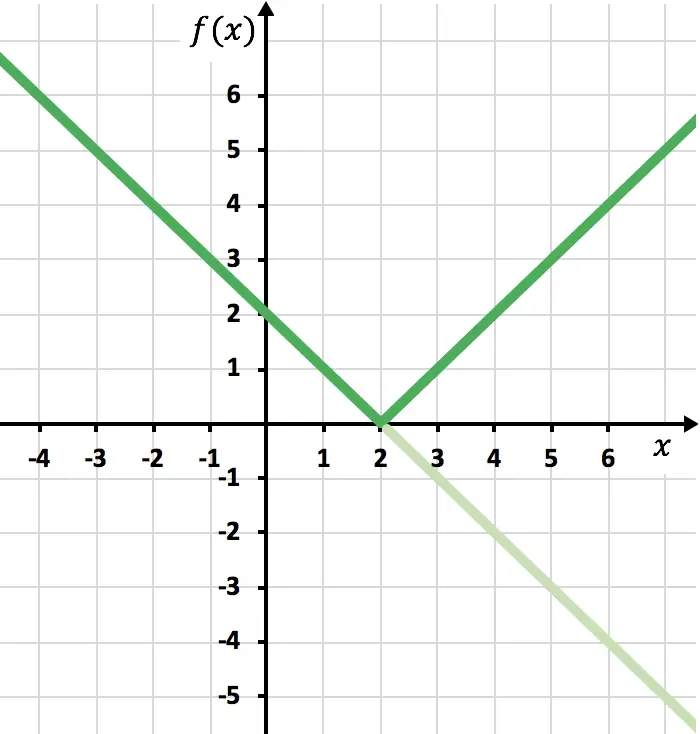
como representar una funcion con valor absoluto

Y finalmente eliminamos el trazo de la función que queda por debajo del eje X:

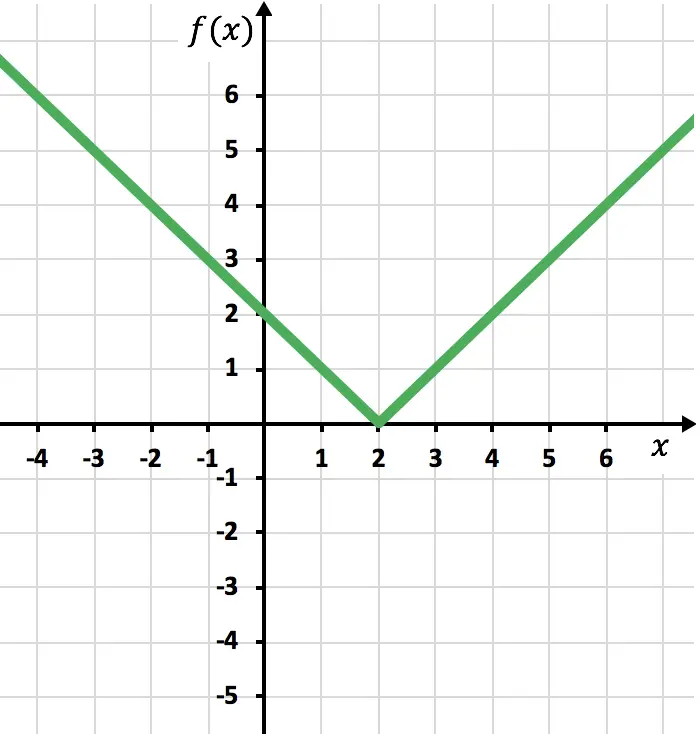
como graficar una funcion con valor absoluto

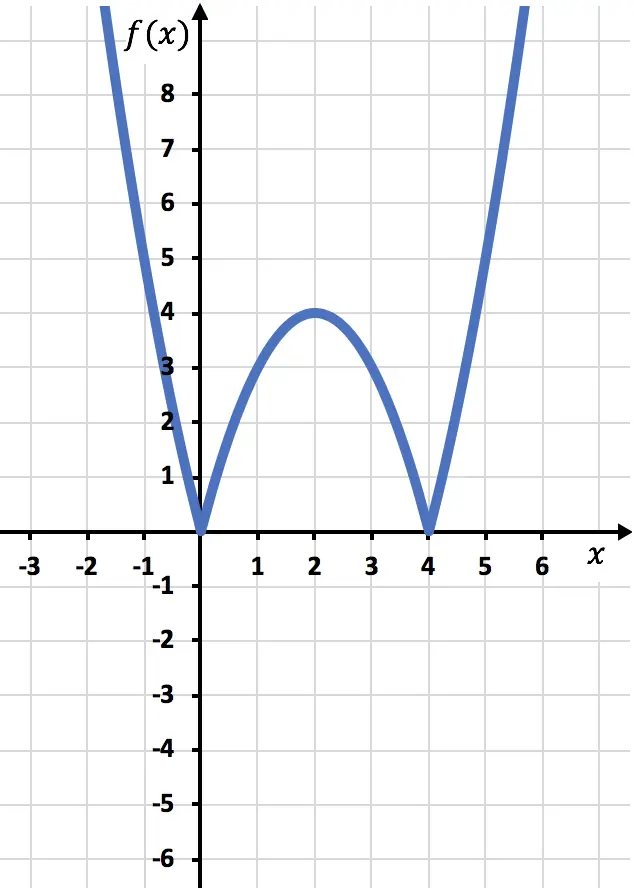
Y de esta manera ya hemos representado la función con valor absoluto. Como has visto, lo único que cambia es que hay que invertir la parte de la función que queda por debajo del eje OX. En consecuencia, la gráfica de cualquier función con valor absoluto siempre quedará en la parte del semieje Y positivo.

Por otro lado, para repasar conceptos, a partir del gráfico se puede deducir que el dominio de la función con valor absoluto anterior son todos los números reales. En cambio, el recorrido o rango de dicha función con valor absoluto son todos los números positivos y el cero.

Ejercicios resueltos de funciones con valor absoluto

Ejercicio 1

Expresa en forma de función definida a trozos la siguiente función con valor absoluto:

$f(x)= \lvert -x+3 \rvert$

Ver solución

En primer lugar, tenemos que mirar cuándo la función es negativa. Para ello, igualamos a cero lo de dentro del valor absoluto y resolvemos la ecuación:

$-x+3=0$

$x=3$

Representamos el valor hallado en la recta:

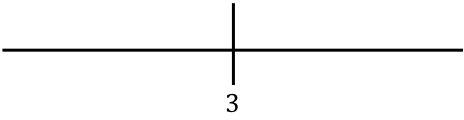
Ahora evaluamos un punto de cada intervalo en la función sin el valor absoluto para saber qué signo tiene realmente la función en cada tramo de la recta:

$x<3$

Cogemos cualquier punto más pequeño que 3, por ejemplo $x=0:$

$-0+3$

$+3$

Positivo

$x>3$

Cogemos cualquier punto más grande que 3, por ejemplo $x=4:$

$-4+3$

$-1$

Negativo

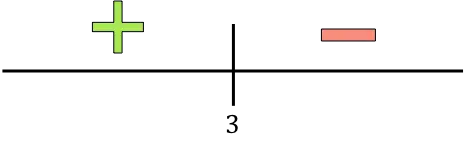
La función sin el valor absoluto sería negativa en el intervalo x>3. De manera que tenemos que expresar la función a trazos cambiándola de signo en ese intervalo:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Ejercicio 2

Halla la expresión en forma de función definida a trozos de la siguiente función con valor absoluto:

$f(x)= \lvert 3x^2-75 \rvert$

Ver solución

Lo primero que debemos hacer es mirar cuándo la función es negativa. Para ello, tenemos que igualar a cero el argumento del valor absoluto y resolver la ecuación:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

Ahora representamos las raíces de la función obtenidas en la recta:

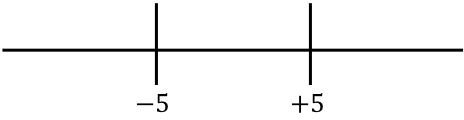
Y miramos qué signo tiene la función sin el valor absoluto en cada intervalo de la recta:

$x<-5$

Cogemos cualquier punto más pequeño que -5, por ejemplo $x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positivo

$-5 < x < 5$

Cogemos cualquier punto entre -5 y +5, por ejemplo $x=0:$

$3(0)^2-75$

$0-75$

$-75$

Negativo

$x>5$

Cogemos cualquier punto más grande que 5, por ejemplo $x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positivo

Por tanto, la función sin el valor absoluto tan solo sería negativa en el intervalo -5<x<5. Por tanto, tenemos que expresar la función por partes cambiando de signo únicamente ese intervalo:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.$

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.$

Ejercicio 3

Realiza la representación gráfica de la siguiente función con valor absoluto:

$f(x)= \lvert 2x-6 \rvert$

Ver solución

Para representar una función con valor absoluto primero debemos representar la función sin el valor absoluto:

$f(x)= 2x+6$

Se trata de una función afín, por lo que tenemos que construir una tabla de valores para graficarla:

$x=0 \longrightarrow f(0)=2\cdot 0-6=-6$

$x=1 \longrightarrow f(1)=2\cdot 1-6=-4$

$x=2 \longrightarrow f(2)=2\cdot 2-6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -6 \\ 1 & -4 \\ 2 & -2 \end{array}$

Representamos los puntos en la gráfica y trazamos la recta:

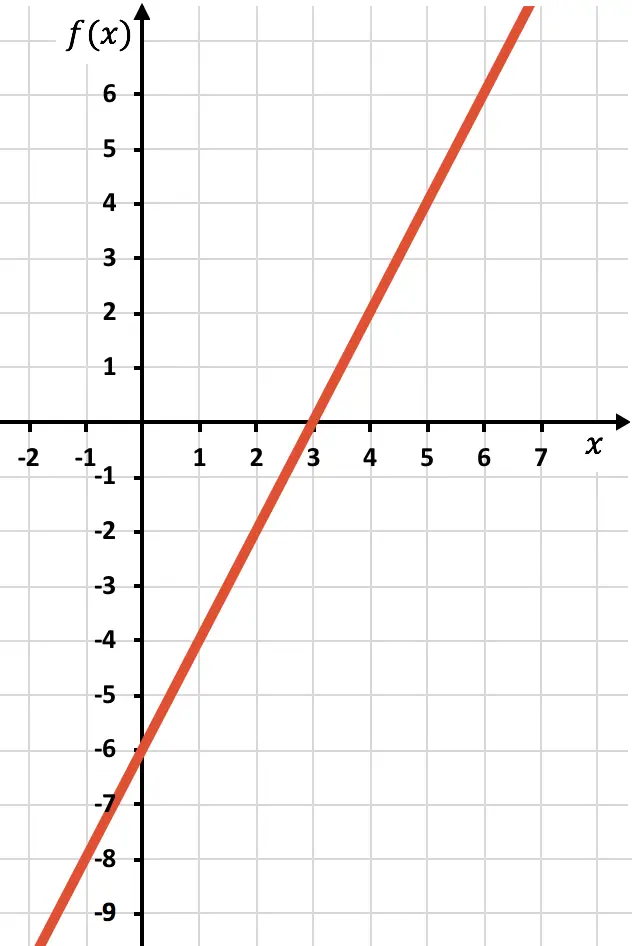
ejercicio resuelto 3 funcion con valor absoluto 1

Ahora tenemos que dibujar la función simétrica donde la función sea negativa, es decir, donde esté por debajo del eje X. Por tanto, invertimos la función desde x=3 hacia atrás:

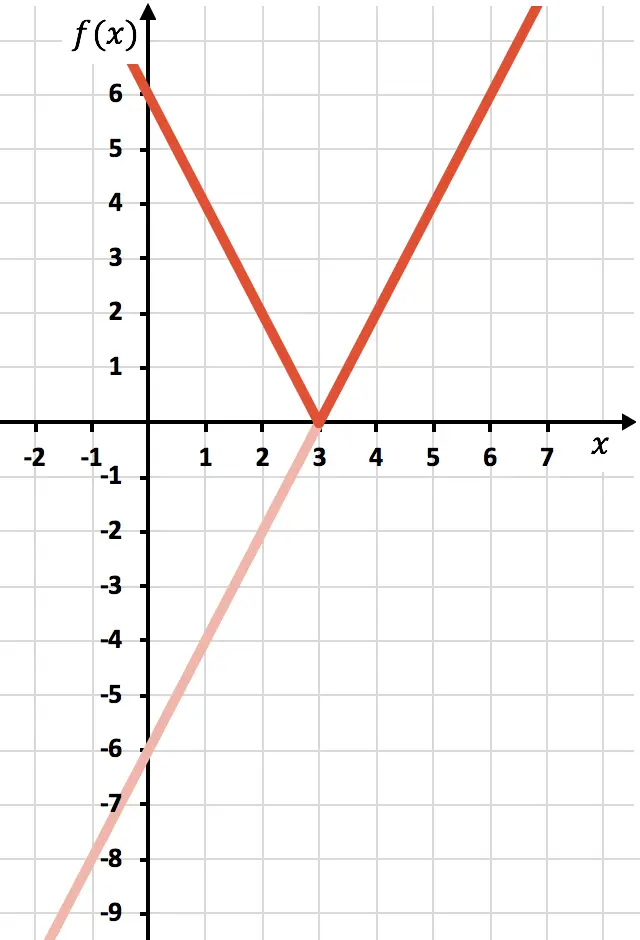
ejercicio resuelto 3 funcion con valor absoluto 2

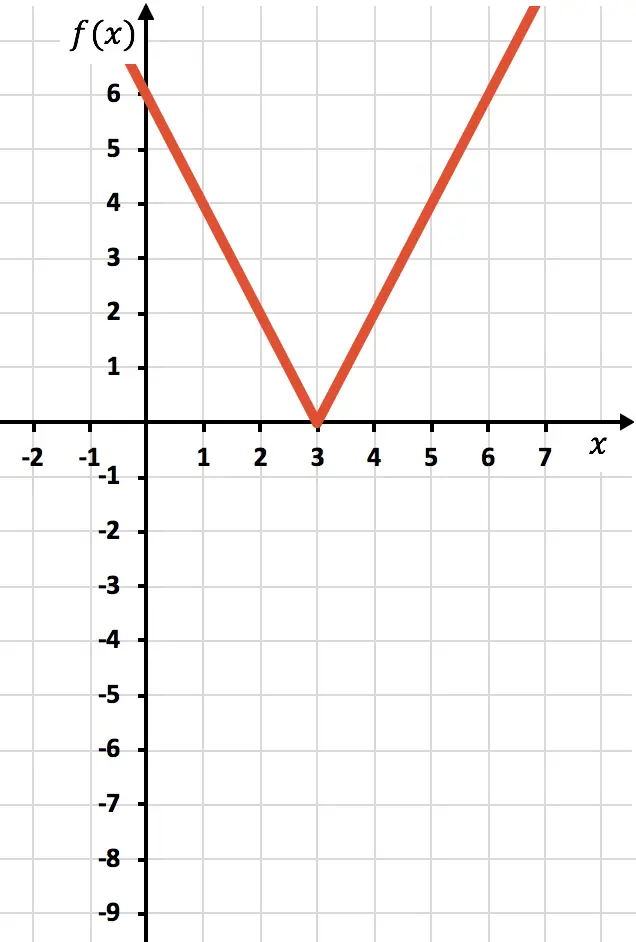
Y, por último, eliminamos la parte de la función que queda por debajo del eje X:

ejercicios resueltos de funciones con valor absoluto

Ejercicio 4

Grafica la siguiente función con valor absoluto:

$f(x)= \lvert x^2-4x \rvert$

Ver solución

Para representar una función con valor absoluto primero debemos dibujar la función sin el valor absoluto.

$f(x)= x^2-4x$

Se trata de una función cuadrática. Por tanto, para representarla tenemos que calcular la coordenada X del vértice de la parábola con su fórmula:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1} = \cfrac{+4}{2} = 2$

Ahora creamos una tabla de valores. Para ello calculamos el valor de $f(x)$ en el vértice y alrededor del vértice:

$x= 2 \ \longrightarrow \ f(2)=2^2-4\cdot 2 = -4$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot 1 = -3$

$x= 3 \ \longrightarrow \ f(3)=3^2-4\cdot 3 = -3$

$x= 0 \ \longrightarrow \ f(0)=0^2-4\cdot 0 = 0 -0 = 0$

$x= 4 \ \longrightarrow \ f(4)=4^2-4\cdot 4 = 0$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & -4 \\ 1 & -3 \\ 3 & -3 \\ 0 & 0 \\ 4 & 0 \end{array}$

Representamos los puntos en el gráfico y trazamos la parábola:

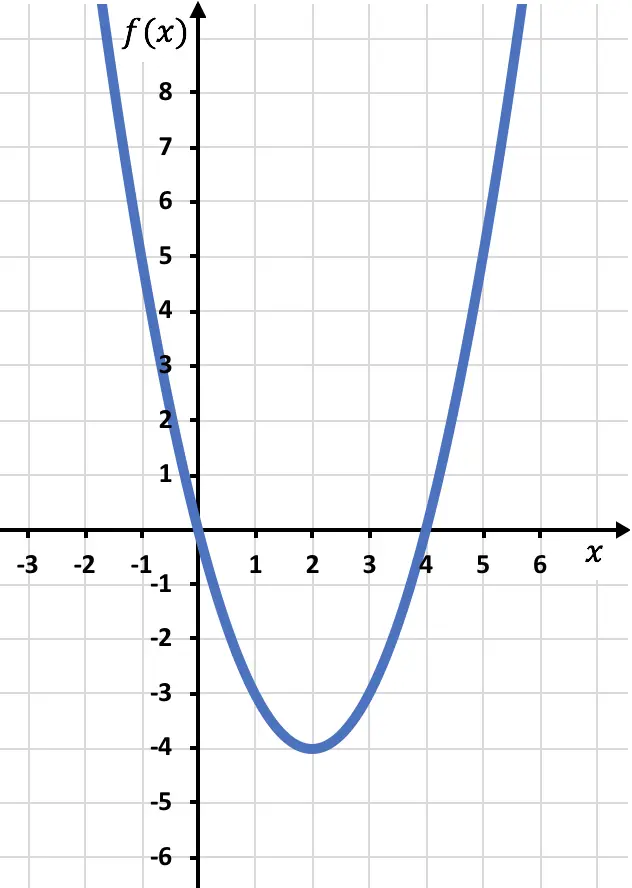
ejemplos de funciones con valor absoluto

Ahora tenemos que trasladar por simetría la función donde sea negativa, es decir, donde esté por debajo del eje OX. Por lo tanto, invertimos la función desde x=0 hasta x=4:

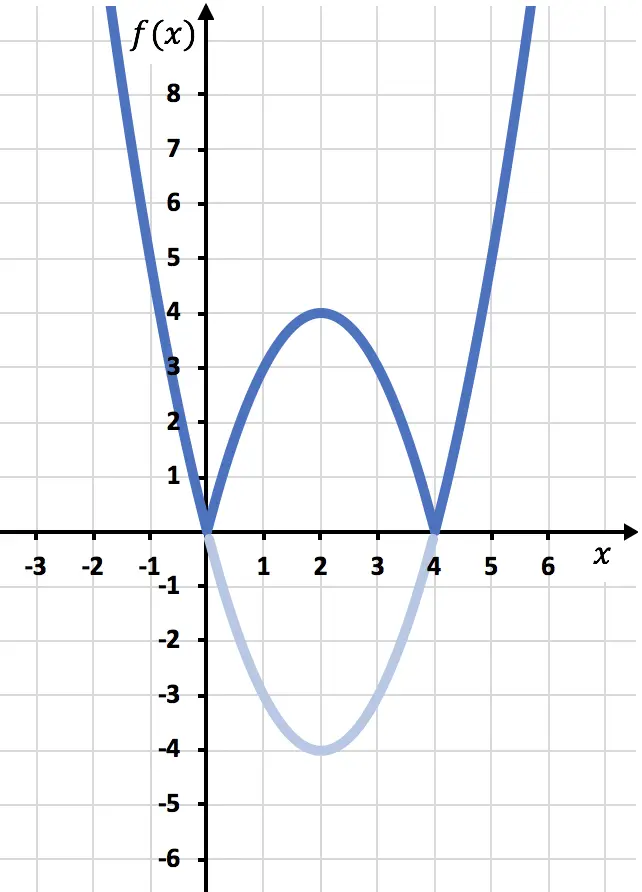
Y finalmente suprimimos la parte de la función que queda por debajo del eje X:

Funciones con valor absoluto

¿Qué son las funciones con valor absoluto?

Cómo definir a trozos una función con valor absoluto

Cómo representar una función con valor absoluto

Ejercicios resueltos de funciones con valor absoluto

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Deja un comentario Cancelar respuesta