Tasa de variación media e instantánea

Aquí te explicamos qué es la tasa de variación, la tasa de variación media y la tasa de variación instantánea. Podrás ver varios ejemplos de cómo calcular las tasa de variación y, además, podrás practicar con ejercicios resueltos paso a paso de la tasa de variación.

¿Qué es la tasa de variación?

En matemáticas, la tasa de variación (TV) de una función es la diferencia de los valores de una función en dos puntos diferentes. Por lo tanto, para calcular la tasa de variación entre dos puntos se deben restar los valores de la función en esos dos puntos.

\text{TV}[a,b]=f(b)-f(a)

Por ejemplo, si dos imágenes de una función son f(2)=1 y f(5)=7, su tasa de variación es:

\text{TV}[2,5]=f(5)-f(2)=7-1=6

Acabamos de ver el significado matemático de la tasa de variación, pero en economía el concepto de tasa de variación significa lo siguiente:

En economía, la tasa de variación entre dos valores es la diferencia entre ellos expresada en forma porcentual, es decir, la tasa de variación de una variable entre distintos periodos es su variación relativa. Por tanto, para calcular la tasa de variación se restan los valores de los dos periodos diferentes y se divide el resultado obtenido entre el valor del periodo inicial.

\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100

Por ejemplo, si el valor de unas acciones han pasado de valer 35€ a costar 50€ en un mes, su tasa de variación será:

\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%

Vistos las dos posibles significados de tasa de variación, en este artículo nos centraremos en entender la definición matemática de tasa de variación. Se pueden distinguir dos tipos de tasas de variación: la tasa de variación media y la tasa de variación instantánea. Seguidamente tienes la explicación de cada tipo.

Tasa de variación media

La tasa de variación media (TVM) de una función en un intervalo es el número de unidades que crece (o decrece) la función por cada unidad que aumenta su variable independiente. Por tanto, la tasa de variación media de una función se calcula dividiendo el crecimiento de la función en un intervalo entre la amplitud de ese mismo intervalo.

\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}

Para que puedas ver cómo se calcula la tasa de variación media, a continuación hemos resuelto un ejemplo paso a paso.

Ejemplo del cálculo de la tasa de variación media de una función

  • Calcula la tasa de variación media en el intervalo [2,5] de la siguiente función:

f(x) = x^2-1

Primero de todo, calculamos el valor de la función en x=2 y x=5:

f(5)= 5^2-1=25-1=24

f(2)=2^2-1=4-1=3

Y luego calculamos la tasa de variación media de la función en el intervalo simplemente aplicando la fórmula:

\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}

\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}

Como el resultado de TVM[2,5] ha sido positivo, significa que la función crece en el intervalo [2,5]. En cambio, si el resultado hubiera sido negativo, significaría que la función decrece en ese intervalo.

Interpretación geométrica de la tasa de variación media

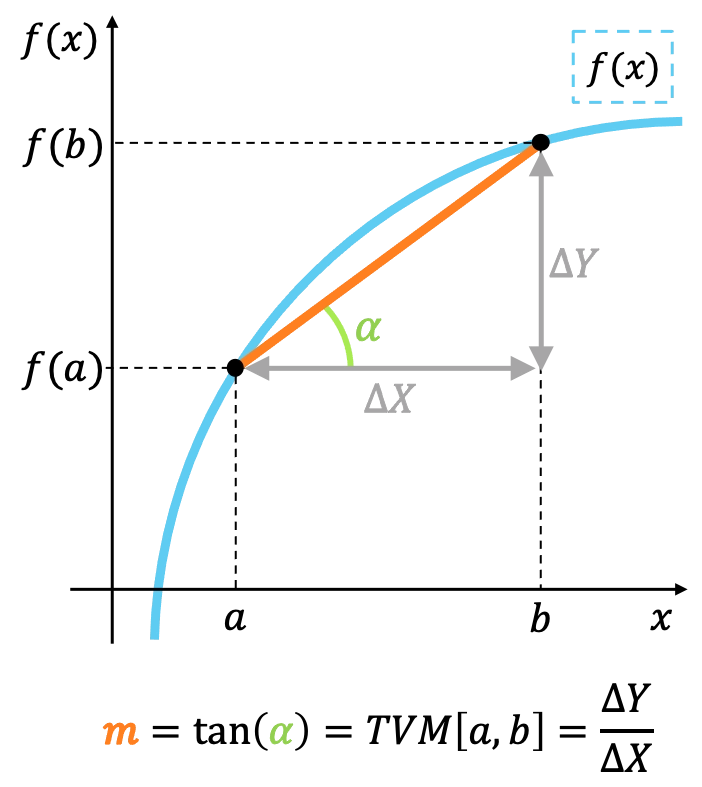
Geométricamente, la tasa de variación media de una función en un intervalo representa la pendiente de la recta que une los puntos extremos del intervalo.

tasa de variacion media

Tasa de variación instantánea

La tasa de variación instantánea (TVI) de una función en un punto es el límite infinitesimal del incremento relativo de la función en un intervalo. Por lo tanto, la tasa de variación instantánea se calcula resolviendo el límite del cociente de f(a+h)-f(a) entre h cuando h tiende a cero.

\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}

El valor de la tasa de variación instantánea puede ser positivo, negativo o nulo, y significa que la función en ese punto crece, decrece o se mantiene igual respectivamente en ese punto.

Ejemplo del cálculo de la tasa de variación instantánea de una función

  • Calcula la tasa de variación instantánea en el punto x=2 de la siguiente función:

f(x) = x^2

Para calcular la tasa de variación instantánea tenemos que aplicar la fórmula:

\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}

\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}

Resolvemos la identidad notable:

\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}

➤ Si no recuerdas las fórmulas de las identidades notables, encontrarás todas las fórmulas en nuestra página web especializada en polinomios: www.polinomios.org

Ahora intentamos resolver el límite:

\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}

Pero nos encontramos con la indeterminación cero entre cero, por tanto:

\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)

➤ Ver: cómo resolver un límite con la indeterminación cero entre cero

Y finalmente resolvemos el límite:

\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}

Por tanto:

\mathbf{TVI} \bm{(2) = 4}

Como el resultado de TVI(2) ha sido positivo, significa que la función crece en x=2. Por contra, si el resultado hubiera sido negativo, significaría que la función decrece en ese punto.

Interpretación geométrica de la tasa de variación instantánea

Geométricamente, la tasa de variación instantánea de una función en punto representa la pendiente de la recta tangente a la función en ese mismo punto.

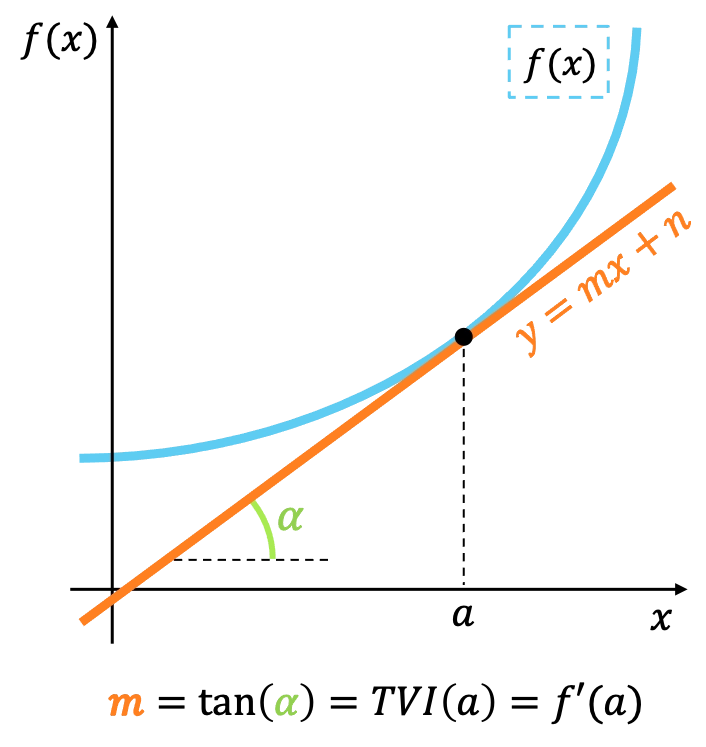
tasa de variacion instantanea

Si te fijas bien, el significado de la tasa de variación instantánea es equivalente al concepto de la derivada de una función. De modo que la tasa de variación instantánea también sirve para calcular el valor de la derivada de una función en un punto.

Ejercicios resueltos de la tasa de variación

Ejercicio 1

Calcula el valor de la tasa de variación de la siguiente función en el intervalo [1,3].

f(x)=x^2-5

En primer lugar, determinamos el valor de la función en los extremos del intervalo:

f(1)=1^2-5=1-5=-4

f(3)=3^2-5=9-5=4

Y ahora aplicamos la fórmula de la tasa de variación:

\text{TV}[a,b]=f(b)-f(a)

\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}

 

Ejercicio 2

Calcula la tasa de variación media (TVM) de la siguiente función en el intervalo [1,4]:

f(x)=2x+1

Primero hacemos el cálculo de las imágenes de la función en x=1 y x=4.

f(4)=2\cdot4+1=9

f(1)=2\cdot 1+1=3

Y aplicamos la fórmula de la tasa de variación media:

\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}

\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}

 

Ejercicio 3

Halla la tasa de variación media de la siguiente función en el intervalo [-1,3]:

f(x)=(x+1)^2

Para determinar la tasa de variación media primero debemos calcular f(-1) y f(3):

f(3)=(3+1)^2=(4)^2=16

f(-1)=((-1)+1)^2=(0)^2=0

Ahora utilizamos la fórmula de la tasa de variación media:

\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}

\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}

 

Ejercicio 4

Calcula la tasa de variación media en el intervalo [2,4] de la función representada en la siguiente gráfica:

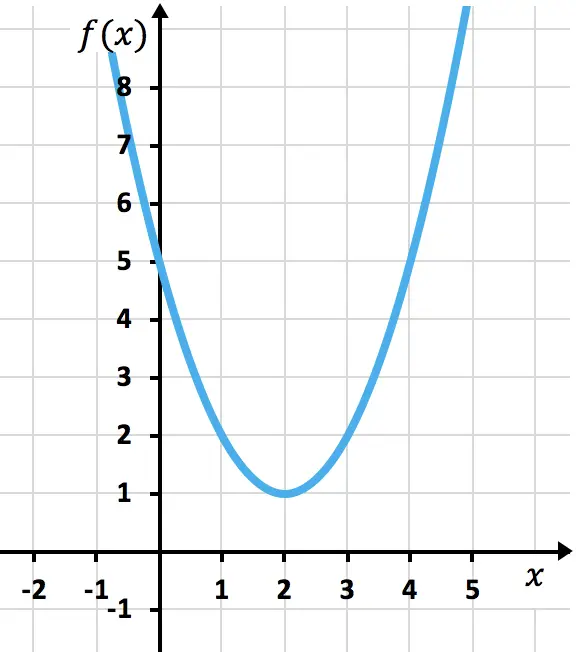
Aplicamos la fórmula de la tasa de variación media:

\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}

\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}

Como vemos en la fórmula, tenemos que hallar el valor de f(4) y de f(2). Y esto se puede hacer fácilmente mirando la representación gráfica de la función:

f(4)=5

f(2)=1

Y ahora que ya sabemos los valores de la función, los sustituimos en la fórmula:

\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}

 

Ejercicio 5

Calcula la tasa de variación instantánea de la siguiente función en el punto x=2:

f(x)=3x

Para determinar la tasa de variación instantánea de la función en el punto x=2 aplicamos su fórmula correspondiente:

\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}

\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}

 

Ejercicio 6

Determina la tasa de variación instantánea (TVI) de la siguiente función en el punto x=1:

f(x)=x^2+1

Aplicamos la fórmula de la tasa de variación instantánea:

\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}

\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}

Entonces, calculamos f(1+h) y f(1):

f(1+h) = (1+h)^2+1

f(1)=1^2+1=1+1=2

Y sustituimos los valores hallados en el límite:

\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}

Resolvemos el producto notable:

\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}

Ahora intentamos resolver el límite:

\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}

Pero nos encontramos con la forma indeterminada cero partido por cero, por tanto, factorizamos el polinomio del numerador de la fracción y simplificamos:

\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)

➤ Si no sabes cómo se resuelve la indeterminación cero entre cero, puedes ver la explicación entera en el enlace de arriba de cómo resolver un límite con la indeterminación cero entre cero

Y, finalmente, resolvemos el límite:

\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}

En resumen, la tasa de variación instantánea de la función en el punto x=1 es igual a 2.

\mathbf{TVI} \bm{(1) = 2}

 

Ejercicio 7

Encuentra la tasa de variación instantánea de la siguiente función en el punto x=2:

f(x)=4x^2-x+3

Primero empleamos la fórmula de la tasa de variación instantánea:

\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}

\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}

Calculamos f(2+h) y f(2):

f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1

f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17

Y sustituimos los valores hallados en el límite:

\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}

Calculamos la igualdad notable:

\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}

Operamos en el numerador:

\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}

Ahora intentamos resolver el límite:

\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}

Pero obtenemos la indeterminación cero partido por cero, por lo que factorizamos los polinomios y simplificamos:

\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)

Y, por último, resolvemos el límite:

\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}

Por tanto:

\mathbf{TVI} \bm{(2) = 15}

 

6 comentarios en “Tasa de variación media e instantánea”

    1. Funciones

      Buenas,

      El cálculo de la tasa de variación media de la función cuadrática en el intervalo propuesto es:

      TV[-1,2]=f(2)-f(-1)=(5\cdot 2)^2-\bigl(5\cdot (-1)\bigr)^2)=100-25=75

  2. Lucia

    Holaa, si en el enunciado de la última pone x=1, ¿por qué se hace con el 2?, ha sido un error o hay calcularlo de alguna manera.
    Muchas gracias por ayudarnooos!!!.

    Responder
    1. Funciones

      Buenas Lucia, si había un simple error en el enunciado, es x=2.

      ¡Muchas gracias por avisar y por tu apoyo! 😉

    1. Funciones

      Buenas Maria,

      La tasa de variación se calcula restando los valores de la función en los dos puntos. En este caso las coordenadas X son 2 y -3, por tanto:

      \begin{aligned}TV(2,-3)&=g(2)-g(-3)\\[2ex]&=\bigl[-9\cdot 2^2+7\cdot2-5\bigr]-\bigl[-9\cdot (-3)^2+7\cdot (-3)-5\bigr]\\[2ex]&=-27-(-107)\\[2ex]&=80\end{aligned}

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *