▷ Resolver la indeterminación cero entre cero (0/0)

En este post te explicamos cómo salvar el límite de una función cuando da la indeterminación 0/0. Además, podrás practicar con ejercicios resueltos de la indeterminación cero entre cero.

Índice

Cómo resolver la indeterminación cero entre cero (0/0)

A continuación, vamos a ver cómo calcular el límite de una función cuando da la indeterminación cero entre cero (0/0). Para ello, calcularemos un ejemplo paso a paso:

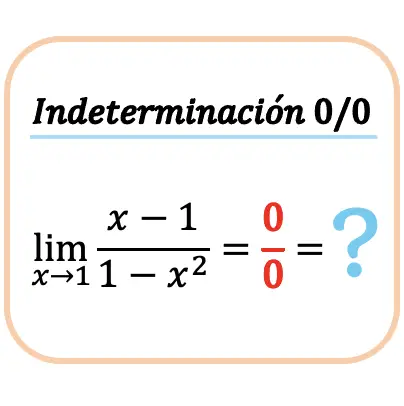
$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

Primero intentamos calcular el límite sustituyendo el valor de x en la función:

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

Pero obtenemos la indeterminación 0 partido por 0.

Cuando el límite de una función en punto da la indeterminación 0/0, debemos factorizar los polinomios del numerador y del denominador y luego simplificar los factores en común.

Por lo tanto, debemos factorizar los polinomios del numerador y del denominador de la fracción. Para ello, utilizamos la regla de Ruffini:

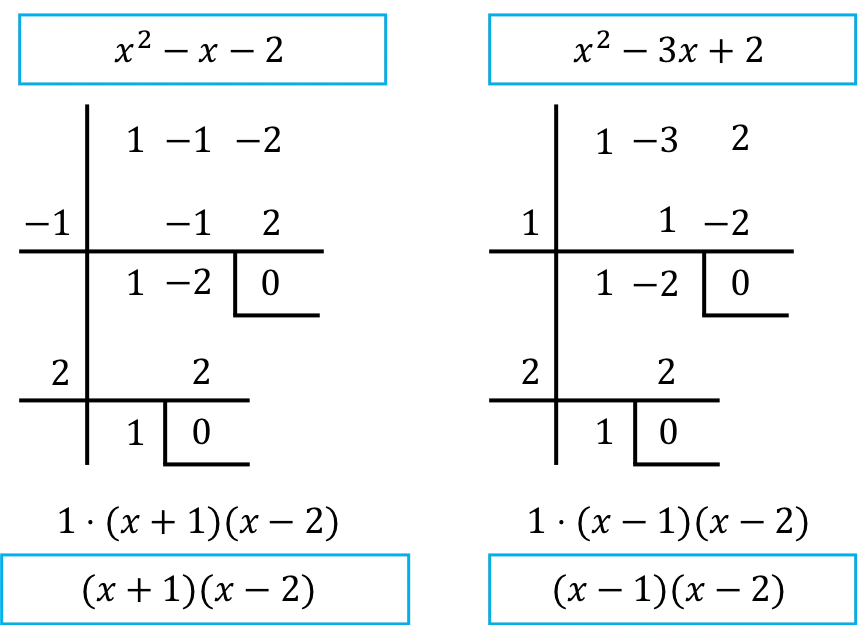
➤ Si no sabes cómo se hace la factorización de un polinomio, te recomendamos que veas la explicación en nuestra página web especializada en polinomios: www.polinomios.org

De manera que, una vez factorizados los polinomios, el límite queda de la siguiente manera:

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

Ahora podemos simplificar el límite eliminado los factores que se repiten en el numerador y en el denominador de la fracción:

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

Y, finalmente, volvemos a calcular el límite:

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

Como puedes ver, una vez hemos factorizado y simplificado los polinomios, resulta muy fácil hallar la solución del límite.

Indeterminación 0/0 con raíces

Acabamos de ver cómo se resuelven las indeterminaciones 0/0 de funciones racionales. Sin embargo, si el límite es de una función irracional (o radical), la indeterminación 0/0 se soluciona de manera diferente.

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

En primer lugar, tratamos de resolver el límite haciendo las operaciones:

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

Pero obtenemos la indeterminación cero sobre cero.

Si el límite de una función con raíces da la indeterminación 0/0, debemos multiplicar el numerador y el denominador de la fracción por el conjugado de la expresión radical.

➤ Recuerda que el conjugado es la misma expresión irracional pero con el signo del medio cambiado.

Entonces, multiplicamos tanto el numerador como el denominador de la fracción por el conjugado de la expresión radical:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

En este tipo de límites, al hacer este paso siempre obtendremos una identidad notable que podremos simplificar. En este caso, en el denominador tenemos el producto de una suma por una diferencia, por tanto:

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

Simplificamos el factor que se repite en el numerador y el denominador:

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

Y de esta forma ya podemos hallar el resultado del límite:

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

Ejercicios resueltos de la indeterminación 0/0

A continuación, hemos preparado varios ejercicios resueltos paso a paso de límites de funciones que den indeterminaciones 0/0. Puedes intentar hacerlos y luego comprobar la solución.

¡Recuerda que puedes preguntarnos cualquier duda que tengas sobre la resolución de los límites en los comentarios!

Ejercicio 1

Calcula el límite de la siguiente función racional en el punto x=-2.

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

Ver solución

Lógicamente, primero intentamos resolver el límite:

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

Pero nos encontramos con la indeterminación 0/0. Por tanto, tenemos que factorizar los polinomios del numerador y del denominador:

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

Ahora simplificamos la fracción quitando el paréntesis que se repite en el numerador y en el denominador:

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

Y, por último, volvemos a calcular el límite con la fracción simplificada:

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

Ejercicio 2

Resuelve el límite de la siguiente función cuando x tiende a -1:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

Ver solución

Primero intentamos resolver el límite como siempre:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

Pero obtenemos la indeterminación 0 entre 0. De manera que debemos hacer la factorización de los 2 polinomios de la fracción:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

Ahora podemos simplificar los polinomios:

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

Y resolvemos el límite:

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

Ejercicio 3

Determina la solución del límite de la siguiente función radical:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

Ver solución

Primero de todo, comprobamos si el límite da algún tipo de indeterminación:

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

El límite da la indeterminación cero partido por cero y tenemos una raíz en la función. Por lo que debemos multiplicar el numerador y el denominador de la fracción por el conjugado de la expresión radical:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

El denominador corresponde al desarrollo de la identidad notable del producto de una suma por una diferencia, así que lo podemos simplificar:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

Sin embargo, aún no podemos simplificar ningún término de la fracción. Por lo tanto, tenemos que factorizar los polinomios:

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

De esta forma podemos simplificar la fracción:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

Y ahora ya podemos determinar el resultado del límite:

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

Ejercicio 4

Calcula el límite cuando x tiende a 0 de la siguiente función radical:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

Ver solución

En primer lugar, intentamos calcular el límite de la función como siempre hacemos:

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

Pero obtenemos la forma indeterminada de 0/0. Por lo tanto, multiplicamos el numerador y el denominador de la función por el conjugado de la expresión irracional:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

Aplicamos la fórmula de la identidad notable correspondiente para simplificar el denominador:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

Ahora factorizamos el binomio del numerador sacando factor común:

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

Simplificamos los factores que se repiten en el numerador y en el denominador de la función:

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

Y, para terminar, resolvemos el límite de la función:

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

Ejercicio 5

Resuelve el siguiente límite aplicando el método de la indeterminación 0/0:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤ Ver: cómo calcular los límites laterales de una función

Ver solución

Primero intentamos resolver el límite:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

Pero en el límite obtenemos la indeterminación cero sobre cero. Por lo tanto, factorizamos los polinomios del numerador y del denominador:

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

Ahora simplificamos la fracción eliminando los factores que se repiten en el numerador y en el denominador:

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

Y volvemos a calcular el límite:

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

Pero ahora nos encontramos con la indeterminación de un número dividido entre 0. Por tanto, tenemos que calcular los límites laterales de la función cuando x tiende a -1.

Primero resolvemos el límite lateral de la función en el punto x=-1 por la izquierda:

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

Y luego calculamos el límite lateral de la función en el punto x=-1 por la derecha:

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

Por tanto, como los dos límites laterales no coinciden, el límite de la función en x=-1 no existe:

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

Indeterminación cero entre cero (0/0)

Cómo resolver la indeterminación cero entre cero (0/0)

Indeterminación 0/0 con raíces

Ejercicios resueltos de la indeterminación 0/0

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Deja un comentario Cancelar respuesta