Función inversa (o recíproca)

En este post te explicamos qué es una función inversa (o recíproca) y cómo calcular la inversa de una función. También encontrarás cómo se puede saber fácilmente si una función tiene inversa o no y las propiedades de este tipo de funciones. Por último, podrás practicar con ejercicios resueltos paso a paso de funciones inversas.

¿Qué es la función inversa?

La función inversa, también llamada función recíproca, es aquella función cuyo dominio es el recorrido de otra función (la función original) y cuyo recorrido es el dominio de la función original. La función inversa de la función f se expresa con el símbolo f-1.

Por lo tanto, la función inversa de f(x) es la función que cumple la siguiente condición:

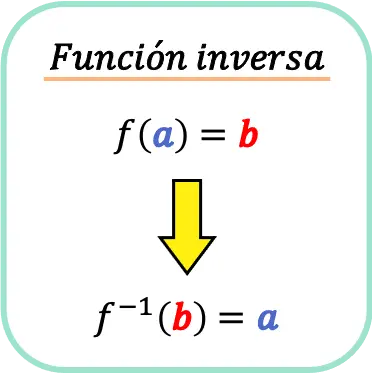
funcion inversa o reciproca

Donde f^{-1} es la función inversa de f.

El concepto de función inversa también se puede definir utilizando la composición de funciones, ya que cualquier función compuesta con su función inversa es igual a la función identidad:

(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x

➤ Ver: ¿qué es la composición de funciones?

De manera que si se cumple la ecuación anterior significa que f^{-1} es la función inversa (o función recíproca) de f.

Ejemplo de función inversa

Vista la definición de función inversa, vamos a resolver un ejemplo para entender mejor su significado.

  • Determina si son inversas entre sí las siguientes funciones:

f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}

Si las dos funciones son inversas entre sí, se cumplirán las siguientes 2 condiciones:

(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x

Por lo tanto, vamos a comprobar si se cumplen ambas ecuaciones. Primero comprobamos (f \circ g)(x) = x:

\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}

➤ Si no entiendes el cálculo que acabamos de hacer debes ir al enlace de arriba de ¿Qué es la composición de funciones?, allí explicamos cómo resolver este tipo de operación con funciones.

De modo que (f \circ g)(x) = x sí se cumple. ✅

Ahora vamos a comprobar la igualdad (g \circ f)(x) = x :

\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}

Y la condición de invertibilidad (g \circ f)(x) = x también se cumple. ✅

En conclusión, como se verifican las dos ecuaciones, las dos funciones son inversas entre sí.

A continuación, puedes ver las dos funciones representadas gráficamente. Fíjate que las gráficas de dos funciones inversas son simétricas respecto a la bisectriz del primer y del tercer cuadrante:

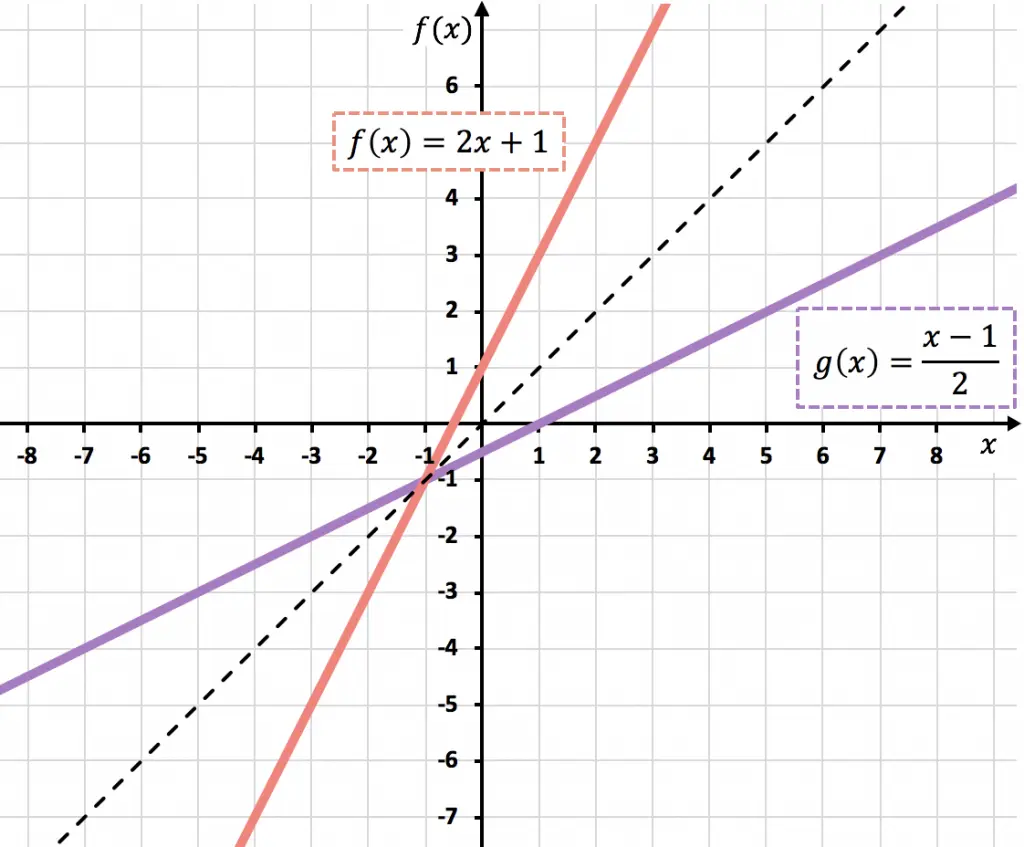
función inversa

Cómo saber si una función tiene inversa

Una función tiene función inversa si se trata de una función inyectiva, es decir, si cada valor del conjunto de su dominio le corresponde solamente un único valor de su recorrido.

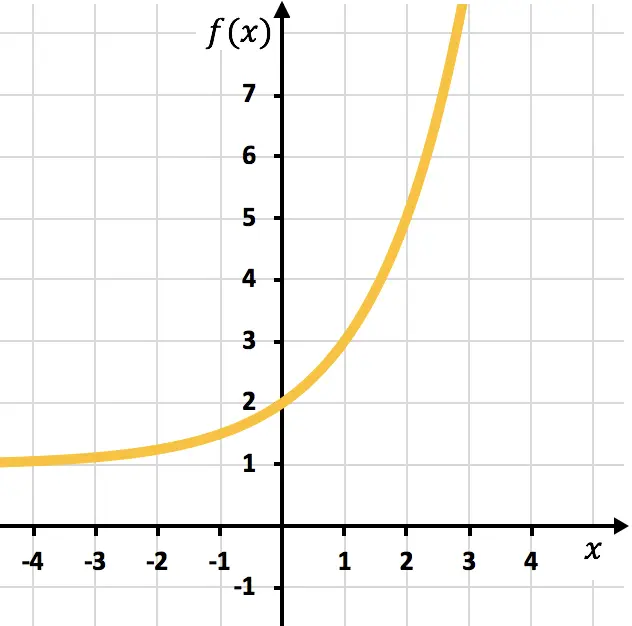
Función exponencial con función inversa

Función cuadrática sin función inversa

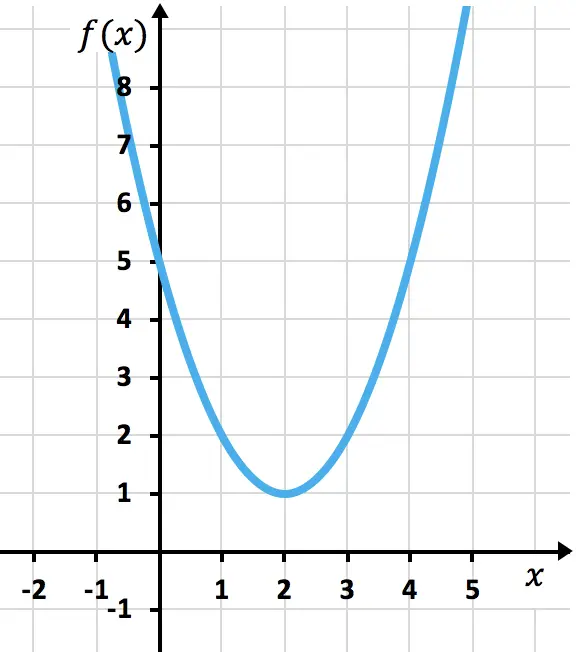
Por ejemplo, la función exponencial de la izquierda sí que tiene función inversa porque a cada x le corresponde un único valor de f(x). En cambio, la función cuadrática de la derecha no posee función inversa ya que tiene varios valores de x cuyas imágenes son iguales (por ejemplo f(1)=f(3)=2).

Asimismo, una función biyectiva consiste en una función que es inyectiva y sobreyectiva al mismo tiempo, por lo tanto, cualquier función biyectiva también tiene función inversa.

Por otro lado, debes tener en cuenta que la función inversa no es lo mismo que la inversa multiplicativa de una función, sino que son dos conceptos diferentes. Para hallar la inversa multiplicativa de una función basta con calcular 1 partido por dicha función.

f^{-1}(x) \neq \cfrac{1}{f(x)}

En el siguiente apartado veremos cómo determinar la función inversa.

Cómo hallar la función inversa

Para calcular la función inversa de una función se deben hacer los siguientes pasos:

  1. Sustituir f(x) por y.
  2. Cambiar todas las x por y, y viceversa.
  3. Despejar la variable y.
  4. Sustiuir la variable y por f-1(x). La función inversa es la expresión hallada de f-1(x).

Para que puedas ver exactamente cómo se calcula la función inversa, determinaremos la inversa de la siguiente función a modo de ejemplo:

f(x) =4x+5

Primero de todo tenemos que sustituir f(x) por y:

y=4x+5

Ahora cambiamos todas las x de la función por y, y viceversa:

y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5

A continuación, despejamos la variable y:

x=4y+5

x-5=4y

\cfrac{x-5}{4}=y

y=\cfrac{x-5}{4}

Y, finalmente, la función inversa de f(x) es la expresión algebraica que hemos obtenido al aislar y:

\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}

Ejercicios resueltos de la función inversa

A continuación, hemos preparado varios ejercicios resueltos paso a paso sobre la función inversa para que puedas practicar.

👉 ¡Recuerda que si no entiendes la resolución de algún ejercicio o quieres que te resolvamos un problema, puedes escribirnos en los comentarios!

Ejercicio 1

Comprueba si las siguientes dos funciones son inversas (o recíprocas) o no:

f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}

Para que las dos funciones sean inversas entre sí, se debe cumplir lo siguiente:

(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x

Por lo que debemos comprobar si se cumplen las dos condiciones. Comprobamos primero (f \circ g)(x)=x :

\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}

Por tanto, (f \circ g)(x) = x sí que se cumple. ✅

Ahora comprobamos la otra composición de funciones (g \circ f)(x)=x :

\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}

De manera que (g \circ f)(x) = x también se cumple. ✅

Como se cumple que  (f \circ g)(x)=x y que (g \circ f)(x)=x , las dos funciones son inversas entre sí.

 

Ejercicio 2

Calcula la inversa (o función recíproca) de la siguiente función polinómica de primer grado:

f(x)=-2x-3

Lo primero que debemos hacer para invertir la función es sustituir el término f(x) por }y:

y=-2x-3

Ahora cambiamos las x por las y, y viceversa:

y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3

Y luego despejamos y:

x =-2y-3

x +3=-2y

\cfrac{x +3}{-2}=y

y = \cfrac{x +3}{-2}

Ya hemos conseguido despejar y. Por tanto, la función inversa de f(x) es:

\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}

 

Ejercicio 3

Invierte la siguiente función polinómica de segundo grado:

f(x)=x^2-1

Para hallar la función inversa seguiremos el procedimiento que hemos visto más arriba. Así que llamaremos y a la función f(x):

y=x^2-1

En segundo lugar, cambiamos la x por la y, y viceversa:

y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1

Y, por último, aislamos la variable y:

x =y^2-1

x+1=y^2

\sqrt{x+1}=y

y=\pm \sqrt{x+1}

Sin embargo, en este caso la función obtenida tiene dos imágenes por cada elemento de su dominio (la imagen positiva y la negativa). En consecuencia, no existe la función inversa de la función del problema.

 

Ejercicio 4

Determina la función inversa (o función recíproca) de la siguiente función racional:

\displaystyle f(x)=\frac{x-1}{2x+3}

En primer lugar, sustituimos f(x) por y:

y=\cfrac{x-1}{2x+3}

Ahora cambiamos las x tanto del numerador como del denominador por y, y viceversa:

y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}

Y a continuación despejamos y:

x=\cfrac{y-1}{2y+3}

La expresión 2y +3 está dividiendo a todo el lado derecho de la ecuación, así que la podemos pasar multiplicando a todo el lado izquierdo de la ecuación:

x\cdot (2y+3)=y-1

2yx+3x=y-1

Ponemos todos los términos con y en un lado de la ecuación, y los otros términos al otro lado:

2yx-y=-3x-1

Para poder despejar }y, extraemos factor común en el lado izquierdo de la ecuación:

y(2x-1)=-3x-1

Y como el factor (2x-1) está multiplicando a todo el lado izquierdo de la ecuación, lo podemos pasar dividiendo a todo el lado derecho:

y=\cfrac{-3x-1}{2x-1}

Ya hemos conseguido despejar y. De forma que la función recíproca de f(x) es:

\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}

 

Propiedades de la función inversa

La función inversa tiene las siguientes características:

  • La función inversa es única, es decir, si una función es invertible, para dicha función solo existe una función inversa.
  • El dominio de la función inversa es el recorrido (o rango) de la función original.
  • Del mismo modo, el recorrido de la función inversa equivale al dominio de la función original.
  • Cualquier función compuesta por su función inversa da como resultado la función identidad (x).

(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x

  • La representación gráfica de una función y la representación gráfica de su función inversa son simétricas respecto a la bisectriz del primer y del tercer cuadrante.
  • La inversa de la función inversa es igual a la función original:

\left(f^{-1}\right)^{-1}=f

  • Invertir una función compuesta es equivalente a calcular la inversa de cada función por separado y luego hacer la composición de las funciones inversas.

(f\circ g)^{-1}=f^{-1}\circ g^{-1}

  • Una función es simultáneamente continua con su función inversa, o dicho de otra forma, si una función es continua también lo será su función inversa.
  • Si una función es derivable y la derivada no se anula en ningún punto f'(x)\neq 0, también será derivable su función inversa.

Además, la derivada de la función inversa se puede calcular aplicando el teorema de la función inversa, cuya fórmula es:

\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}

2 comentarios en “Función inversa (o recíproca)”

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *