En esta página verás cuál es la derivada del arcosecante (fórmula). Encontrarás ejercicios resueltos de derivadas del arcosecante de una función.
Índice
Fórmula de la derivada del arcosecante
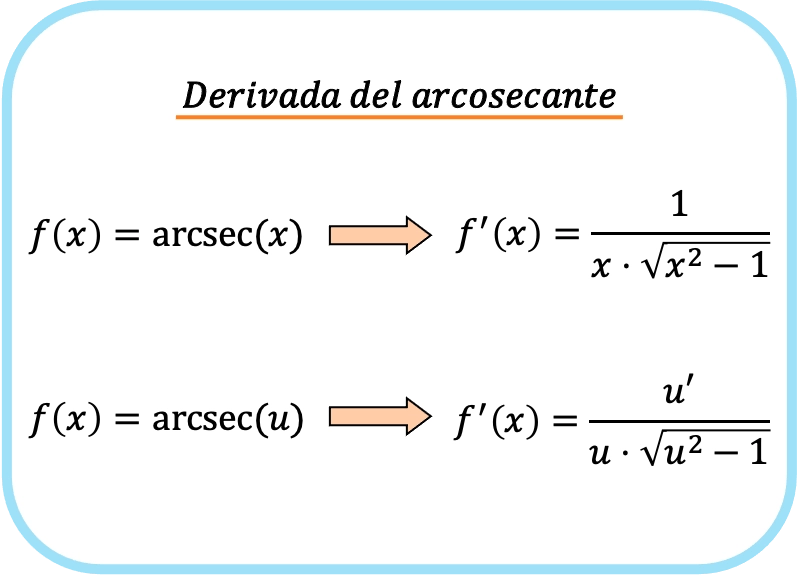
La derivada del arcosecante de x es uno partido por el producto de x por la raíz de x al cuadrado menos 1.
Por lo tanto, la derivada del arcosecante de una función es igual al cociente de la derivada de esa función dividido por la función por la raíz de dicha función al cuadrado menos uno.
Evidentemente, la segunda fórmula es parecida a la primera fórmula, la única diferencia entre ambas es que en la segunda fórmula se aplica la regla de la cadena.
Aunque parezca extraño porque son funciones inversas, la derivada del arcosecante no se parece en nada a la derivada de la secante. Puedes ver la fórmula de la derivada de la secante haciendo click aquí:
➤ Ver: derivada de la secante
Ejemplos de la derivada del arcosecante
Ejemplo 1
En este ejemplo veremos cuánto es la derivada del arcosecante de la función lineal 7x.
Para hallar la derivada del arcosecante debemos aplicar su fórmula correspondiente, que es la siguiente:
La derivada de la función 7x es 7, por tanto, la derivada del arcosecante de la función 7x es:
Ejemplo 2
En este segundo ejemplo derivaremos el arcosecante de una función potencial.
Como en el argumento de la función arcosecante hay un término diferente de x, debemos aplicar la regla de la derivada del arcosecante con la regla de la cadena para hacer la derivación de toda la función.
Entonces, en el numerador escribimos la derivada del argumento de la función, y en el denominador reescribimos la función potencial y la multiplicamos por la raíz cuadrada de la función del argumento elevada a la 2 menos 1:
