Aquí encontrarás cómo derivar la secante de una función. Además, podrás ver varios ejercicios resueltos paso a paso de la derivada de la secante. Y, finalmente, hallarás la demostración de la fórmula de este tipo de derivada trigonométrica.
Índice
¿Cuál es la derivada de la secante?
La derivada de la secante de x es igual al producto de la secante de x por la tangente de x.
Aplicando las fórmulas trigonométricas, también se puede definir la derivada de la secante de x como el cociente del seno de x entre el cuadrado del coseno de x.
Y si aplicamos la regla de la cadena, la derivada de la secante de un función es el producto de la secante de la función por la tangente de la función por la derivada de la función.
En resumen, la fórmula de la derivada de la función secante es la siguiente:
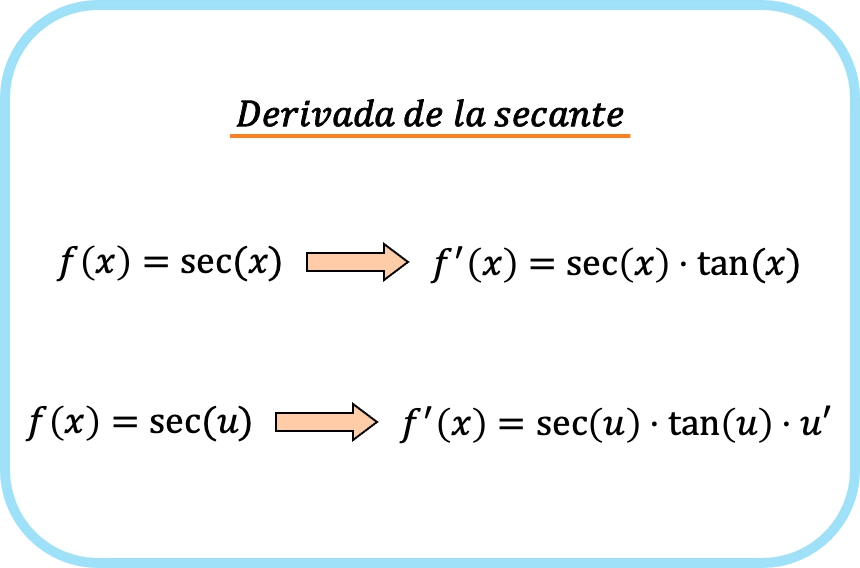
Ejemplos de la derivada de la secante
Una vez hemos visto cuál es la fórmula de la derivada de la secante, vamos a resolver varios ejemplos de este tipo de derivadas trigonométricas.
Ejemplo 1: Derivada de la secante de 2x
En este ejemplo veremos cuánto es la derivada de la secante de 2x:
Para derivar la secante de la función 2x, debemos emplear su fórmula correspondiente. Además, en el argumento de la secante tenemos una función distinta de x, por lo que tenemos que aplicar la regla de la cadena.
La función 2x es lineal, así que su derivada es 2. Por lo tanto, para hallar la derivada simplemente debemos sustituir en la fórmula la u por 2x y la u’ por 2:
Ejemplo 2: Derivada de la secante de x al cuadrado
En este ejercicio veremos cuánto vale la derivada de la secante de x al cuadrado:
Para derivar la secante de una función puedes utilizar cualquiera de las dos fórmulas vistas arriba, pero en este caso derivaremos la función con la fórmula de la multiplicación entre la secante y la tangente.
La derivada de x elevada a 2 da 2x, de modo que la derivada de la secante de x al cuadrado es:
Ejemplo 3: Derivada de la secante al cubo de un polinomio
La regla de la derivada de la secante de una función es:
Pero en este caso debemos derivar una función compuesta, ya que la secante está elevada a la tres y, además, en su argumento tenemos una función polinómica. De manera que para hacer la derivación de toda la función tenemos que aplicar la regla de la cadena:
Ejercicios resueltos de la derivada de una secante
Deriva las siguientes funciones secante:
Demostración de la fórmula de la derivada de la secante
A continuación, vamos a demostrar la fórmula de la derivada de la secante. Aunque obviamente no es necesario que te sepas de memoria la demostración, siempre está bien entender de dónde vienen las fórmulas.
Matemáticamente, la definición de la secante es el inverso multiplicativo del coseno:
Por tanto, podemos intentar derivar la secante utilizando la regla del cociente:
Y, como hemos visto en el primer apartado, la expresión anterior se puede convertir en la fórmula de la derivada de la secante. Para ello, separamos la fracción en dos fracciones diferentes:
La división del seno entre el coseno es equivalente a la tangente, por tanto, sustituimos dicho cociente por la tangente:
Según la definición matemática de la función secante, el coseno es su inverso multiplicativo. De manera que reemplazando uno partido por el coseno por la secante llegamos a la fórmula de su derivada:
