▷ Derivada de una función lineal (ejercicios resueltos)

En este post te mostramos cuánto es la derivada de una función lineal. Además, resolvemos varios ejemplos de derivadas de funciones lineales y demostramos la fórmula de este tipo de derivadas. Incluso encontrarás ejercicios resueltos de derivadas de funciones lineales.

Índice

¿Cuál es la derivada de una función lineal?

La derivada de una función lineal es el coeficiente del término de primer grado, es decir, la derivada de una función lineal f(x)=Ax+B es igual a A.

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

El término independiente se elimina de la derivada porque la derivada de una constante es igual a cero. Y, por otro lado, la derivada de un término de primer grado es el coeficiente de dicho término. Por lo que la derivada de la suma de estos dos tipos de funciones es el coeficiente del término lineal.

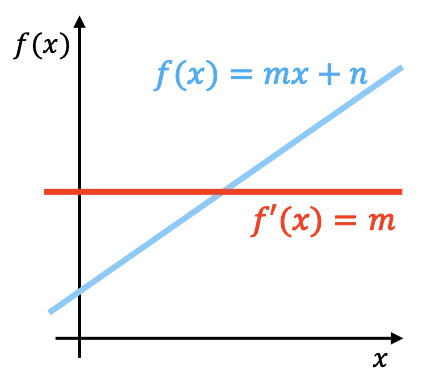
Geométricamente, la derivada de una función lineal es la pendiente de dicha función. En la gráfica anterior puedes ver representadas una función lineal junto con su derivada.

Ejemplos de derivadas de funciones lineales

Vista la definición de la derivada de una función lineal, vamos a calcular varios ejemplos de funciones lineales para acabar de entender el concepto:

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Ten en cuenta que la derivada de la función lineal sigue siendo el número que acompaña la variable x cuando la función no tiene término independiente, o dicho con otras palabras, si solamente tiene un término de primer grado. Por ejemplo:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$

Por lo tanto, la derivada de una función lineal es una función sin variable independiente, un simple número.

Demostración de la derivada de una función lineal

A continuación, vamos a demostrar la fórmula de la derivada de una función lineal.

Sea f una función lineal cualquiera:

$f(x)=Ax+B$

La fórmula para calcular de la derivada de una función en un punto es:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$

De manera que si calculamos el límite anterior para una función lineal obtenemos:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=\frac{A(a+h)+B-(A\cdot a+B)}{h}$

Resolvemos el paréntesis:

$\displaystyle f'(a)=\frac{Aa+Ah+B-Aa-B}{h}$

Operamos en el numerador:

$\displaystyle f'(a)=\frac{Ah}{h}$

Y, por último, simplificamos la fracción:

$\displaystyle f'(a)=A$

En conclusión, la derivada de una función lineal es igual al coeficiente del término de primer grado en cualquier punto. Así pues, queda demostrada la fórmula de la derivada de una función lineal.

Ejercicios resueltos de derivadas de funciones lineales

Calcula las derivadas de las siguientes funciones lineales:

$\text{A)}\ f(x)=2x-25$

$\text{B)}\ f(x)=x+3$

$\text{C)}\ f(x)=-9x-1$

$\text{D)}\ f(x)=\cfrac{1}{2}x+7$

$\text{E)}\ f(x)=5x$

$\text{F)}\ f(x)=\sqrt{7}x+\frac{3}{4}$

Ver solución

Para derivar una función lineal simplemente debemos eliminar el término constante y la variable de la función, de modo que solo quede el coeficiente del término lineal. Por tanto:

$\text{A)}\ f'(x)=2$