▷ Concavidad y convexidad de una función (curvatura)

Aquí encontrarás qué es la concavidad y la convexidad de una función y cómo saber si una función es cóncava o convexa. Además, podrás practicar con ejercicios resueltos paso a paso de la curvatura de una función.

Índice

¿Qué es la concavidad y la convexidad de una función?

La concavidad y la convexidad de una función se refiere a la curvatura que tiene la gráfica de una función. Una función cóncava es una función cuya representación gráfica tiene forma de montaña, y una función convexa es una función cuya gráfica tiene forma de valle.

En el párrafo anterior se han definido las funciones cóncavas y convexas de manera informal para que sea más fácil de entender, pero la definición matemática de función cóncava y función convexa son las siguientes:

Función cóncava: cuando el segmento que une dos puntos cualesquiera de la función queda por debajo de la curva.
Función convexa: cuando el segmento que une dos puntos cualesquiera de la función queda por encima de la curva.

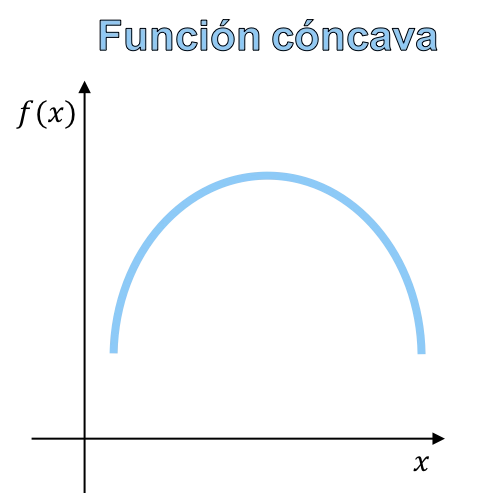
En definitiva, la diferencia entre una función cóncava y una función convexa es la forma que tiene la función y, por lo tanto, se puede distinguir entre concavidad y convexidad a partir de la gráfica de la función.

Sin embargo, una función no tiene por qué ser cóncava o convexa en todo su dominio, sino que también puede ser cóncava en un intervalo y ser convexa en otro intervalo.

Nota: La comunidad matemática aún no está totalmente de acuerdo y, por tanto, hay profesores que lo dicen al revés: llaman función cóncava la que tiene forma de $\bm{\cup}$ , y función convexa la que tiene forma de $\bm{\cap}$ . En cualquier caso, lo importante es saber de qué forma es la función, independientemente del nombre.

Cómo estudiar la curvatura de una función

Estudiar la curvatura de una función consiste en hallar la concavidad y convexidad de la función, es decir, en averiguar los intervalos en los que la función es cóncava y los intervalos en los que la función es convexa.

Entonces, para estudiar la curvatura de una función se deben hacer los siguientes pasos:

Hallar los puntos que no pertenecen al dominio de la función.
Calcular la primera derivada y la segunda derivada de la función.
Hallar las raíces de la segunda derivada, es decir, calcular los puntos que anulan la segunda derivada resolviendo $f''(x)=0$ .
Hacer intervalos con las raíces de la derivada y los puntos que no pertenecen al dominio de la función.
Calcular el valor de la segunda derivada en un punto de cada intervalo.
De manera que el signo de la segunda derivada determina la concavidad o convexidad de la función en ese intervalo:
- Si la segunda derivada de la función es positiva, la función es convexa en ese intervalo.
- Si la segunda derivada de la función es negativa, la función es cóncava en ese intervalo.

Ejemplo de cómo hallar la curvatura de una función

A continuación, vamos a resolver un ejemplo paso a paso para que veas cómo se calculan los intervalos de concavidad y convexidad de una función.

Estudia la concavidad y convexidad de la siguiente función:

$f(x)=x^3-3x$

Lo primero que debemos hacer es calcular el dominio de la función. En este caso tenemos una función polinómica, por tanto, el dominio de la función son todos los números reales:

$\text{Dom } f= \mathbb{R}$

Una vez hemos calculado el dominio de la función, debemos estudiar en qué puntos se anula la segunda derivada de la función.

Así que calculamos la primera derivada de la función:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

Luego hallamos la segunda derivada de la función:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

Y ahora igualamos la segunda derivada a 0 y resolvemos la ecuación:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

Una vez hemos calculado el dominio de la función y $f''(x)=0$ , representamos en la recta todos los puntos críticos encontrados. En este caso no hemos hallado ningún punto crítico del cálculo del dominio de la función, pero si hemos obtenido un punto que anula la segunda derivada de la función:

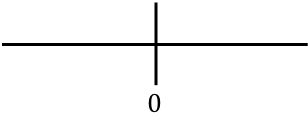
Y ahora evaluamos el signo de la segunda derivada en cada intervalo, para saber si la función es cóncava o convexa. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos críticos) y miramos qué signo tiene la segunda derivada en ese punto:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Por último, deducimos los intervalos de concavidad y convexidad de la función. Si la segunda derivada es positiva significa que la función es convexa $(\bm{\cup})$ , y si la segunda derivada es negativa significa que la función es cóncava $(\bm{\cap})$ . De modo que los intervalos de concavidad y convexidad de la función son:

Convexa $(\bm{\cup})$ : $\bm{(0,+\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-\infty,0)}$

Ejercicios resueltos de la concavidad y convexidad de una función

Ejercicio 1

Calcula los intervalos de concavidad y convexidad de la siguiente función polinómica:

$f(x) = x^3-3x^2-2x$

Ver solución

La función del ejercicio es un polinomio, por lo que el dominio de la función son todos los números reales:

$\text{Dom } f= \mathbb{R}$

Después de determinar el dominio de la función, la derivamos:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

Luego hallamos la segunda derivada de la función:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

Y ahora igualamos la segunda derivada a 0 y resolvemos la ecuación:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

Una vez hemos calculado el dominio de la función y hemos resuelto $f''(x)=0$ , representamos en la recta numérica todos los puntos singulares encontrados:

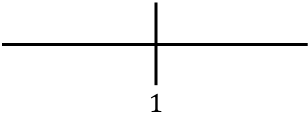
Y ahora cogemos un punto perteneciente a cada intervalo y miramos qué signo tiene la segunda derivada en ese punto:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

Cuando la segunda derivada es mayor que cero quiere decir que la función es convexa $(\bm{\cup})$ , pero cuando la segunda derivada es negativa implica que la función es cóncava $(\bm{\cap})$ . En consecuencia, los intervalos de concavidad y convexidad son:

Convexa $(\bm{\cup})$ : $\bm{(1,+\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-\infty,1)}$

Ejercicio 2

Estudia la curvatura de la siguiente función racional:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Ver solución

Primero tenemos que calcular el dominio de la función. Como se trata de una función racional, igualamos a cero el denominador para ver qué números no pertenecen al dominio de la función:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Esto significa que cuando x sea -2 o +2, el denominador será 0. Y, en consecuencia, la función no existirá. Así que el domino de la función son todos los números excepto x=-2 y x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

En segundo lugar, calculamos la primera derivada de la función:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Y luego resolvemos la segunda derivada:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Todos los términos están multiplicados por $(x^2-4)$ . Así que podemos simplificar la fracción:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Ahora calculamos las raíces de la segunda derivada de la función:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

El término $\left(x^2-4\right)^3$ está dividiendo a todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Extraemos factor común:

$x(8x^2+96)=0$

Para que la multiplicación valga 0, uno de los dos elementos de la multiplicación tiene que ser zero. Por lo tanto, igualamos cada factor a 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$ no tiene solución, ya que no existe la raíz negativa de un número real.

Ahora representamos en la recta todos los puntos críticos obtenidos, es decir, los puntos que no pertenecen al dominio (x=-2 y x=+2) y los que anulan la segunda derivada (x=0):

Y evaluamos el signo de la segunda derivada en cada intervalo, para saber si la función es cóncava o convexa. De manera que cogemos un punto de dentro de cada intervalo y miramos qué signo tiene la segunda derivada en ese punto:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Si la segunda derivada es positiva significa que la función es convexa $(\bm{\cup})$ , y si la segunda derivada es negativa significa que la función es cóncava $(\bm{\cap})$ . Por tanto, los intervalos de concavidad y convexidad son:

Convexa $(\bm{\cup})$ : $\bm{(-2,0)\cup (2,+\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-\infty,-2)\cup (0,2)}$

Ejercicio 3

Una función $f(x)$ tiene un extremo relativo en $x=3$ . Y, además, la función es convexa $(\cup )$ en ese mismo punto. Razona si el extremo relativo es un mínimo o un máximo.