Transformaciones de funciones: Traslaciones, Simetría, Expansión y Compresión

En esta página se explica qué son las transformaciones de las funciones y cómo hallarlas. Hay tres tipos de transformaciones: traslaciones (o desplazamientos), simetrías y expansiones (o contracciones). También encontrarás ejercicios resueltos paso a paso para que puedas practicar y entender los conceptos sin que te quede ninguna duda.

¿Qué son las transformaciones de funciones?

A veces nos pueden pedir graficar funciones elementales muy parecidas a otras que ya conocemos. Pues, en vez de representar de nuevo la función similar, se pueden utilizar técnicas para pasar de la representación de una función a otra de manera fácil y rápida.

Así pues, las transformaciones de funciones son técnicas que nos permiten pasar de la representación gráfica de una función a la representación gráfica de otra función muy similar mediante operaciones elementales.

Básicamente existen tres tipos de transformaciones de funciones elementales:

  • Traslaciones o desplazamientos: se puede desplazar una función verticalmente y horizontalmente.
  • Reflexiones o simetrías: se puede hacer reflejar una función usando como eje de simetría el eje X o el eje Y.
  • Expansiones y compresiones: se puede engrandecer o empequeñecer una función.

Una vez hemos visto el concepto de transformación de una función, vamos a profundizar en cada tipo de modificación.

Traslaciones o desplazamientos de funciones

Primero empezaremos con los desplazamientos de funciones. Existen dos tipos: las traslaciones verticales y las traslaciones horizontales.

Traslación o desplazamiento vertical de una función

Para trasladar o desplazar una función verticalmente (a lo largo del eje Y) hay que sumar o restar una constante a la función:

Desplazamos una función k unidades hacia arriba sumando k a al función: \bm{f(x)+k}

Desplazamos una función k unidades hacia abajo restando k a al función: \bm{f(x)-k}

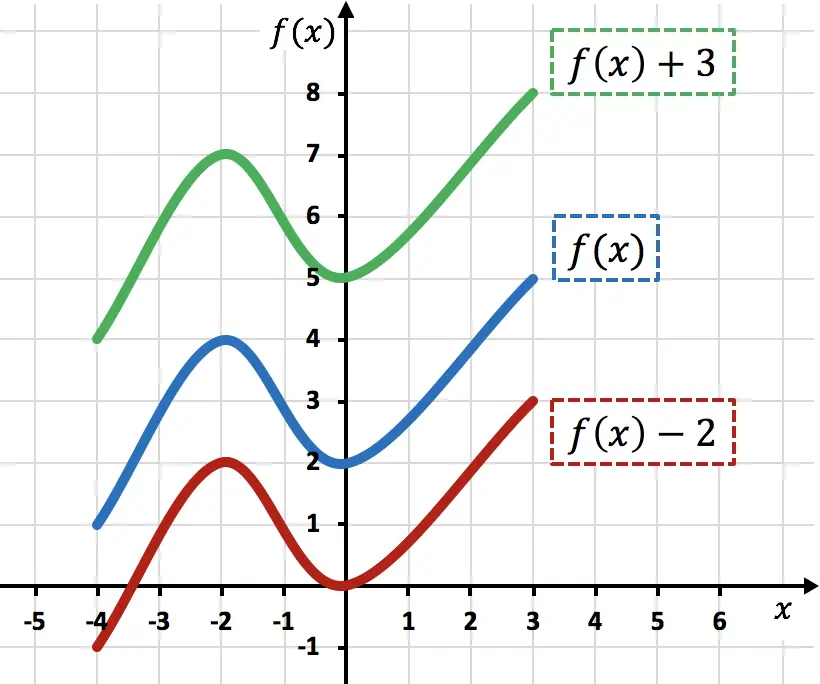
Traslacion o desplazamiento vertical de una funcion

Como puedes ver en el gráfico, al sumar una constante a cualquier función, esta se desplaza las unidades sumadas hacia arriba (función verde). En cambio, al restar un número a cualquier función, esta se desplaza las unidades restadas hacia abajo (función roja).

Fíjate que en este tipo de movimientos solo se modifican las coordenadas Y de los puntos de la función, mientras que las coordenadas X permanecen iguales.

Traslación o desplazamiento horizontal de funciones

Para trasladar o desplazar una función horizontalmente (a lo largo del eje X) hay que sumar o restar una constante a la variable independiente x:

La gráfica de \bm{f(x+k)} es la gráfica de f(x) desplazada k unidades hacia la izquierda.

La gráfica de \bm{f(x-k)} es la gráfica de f(x) desplazada k unidades hacia la derecha.

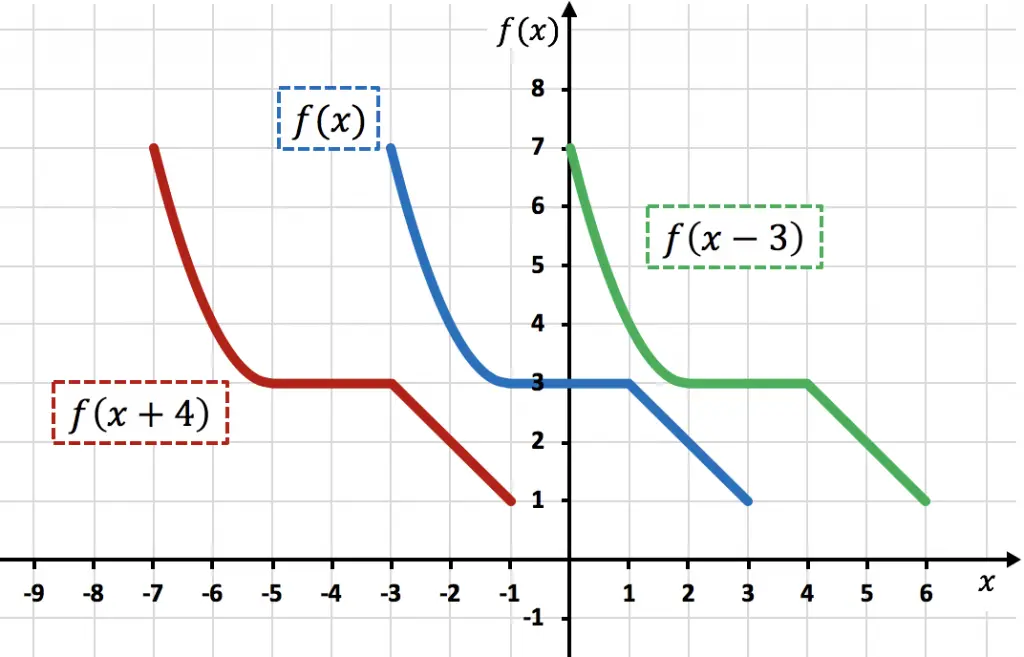
Traslacion o desplazamiento horizontal de una funcion

Como puedes ver en el gráfico, al sumar una constante directamente a la variable x, la función se desplaza las unidades sumadas hacia la izquierda (función roja). Por contra, al restar un número a la variable x, la función se desplaza las unidades restadas hacia la derecha (función verde).

Fíjate que en este tipo de movimientos únicamente se alteran las coordenadas X de los puntos de la función, mientras que las coordenadas Y continuan con el mismo valor.

Ejemplo de cómo trasladar o desplazar una función

  • Desplaza 4 unidades hacia arriba y 3 unidades hacia la derecha la siguiente función:

f(x)=x^2

Para desplazar la función 4 unidades hacia arriba tenemos que sumar 4 unidades a la función:

f(x) + 4 = x^2 + 4

Y para, además, desplazar la función 3 unidades hacia la derecha debemos calcular f(x-3). Por lo tanto, donde hay una x ponemos x-3 :

f(x-3) = (x-3)^2 + 4

Así que la función desplazada 4 unidades hacia arriba y 3 unidades hacia la derecha es:

\bm{f(x) = (x-3)^2 + 4}

A continuación tienes representadas gráficamente la función original y la transformada para que puedas ver la diferencia entre ellas:

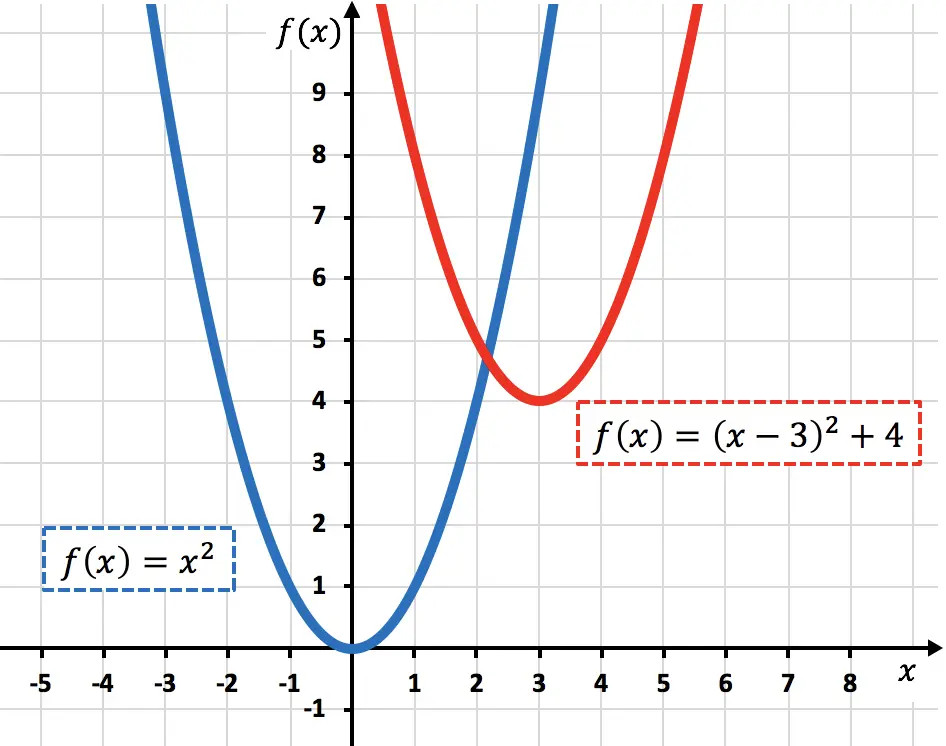
ejemplo de traslacion o desplazamiento de una funcion

Hay matemáticos que llaman desplazamiento o traslación oblicua cuando se producen los dos tipos de movimientos a la vez.

Reflexión o simetría de una función respecto los ejes de coordenadas

Podemos representar la función simétrica respecto cualquier eje cartesiano de la siguiente manera:

Para reflejar una función respecto el eje de las abscisas tenemos que cambiar de signo la función, es decir, debemos calcular \bm{-f(x)}.

Para reflejar una función respecto el eje de las ordenadas tenemos que negar la variable independiente x, es decir, debemos calcular \bm{f(-x)}.

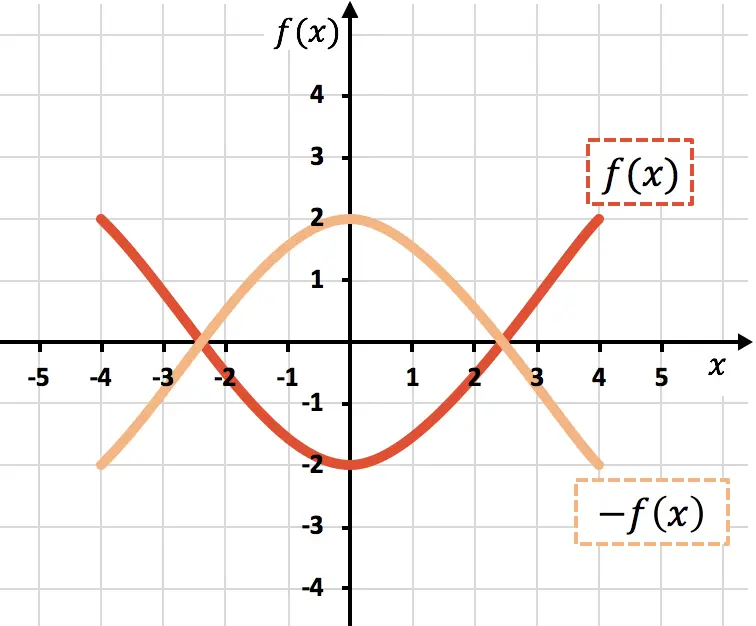
reflexion o simetria respecto el eje X

Como puedes ver en la gráfica anterior, al multiplicar una función por -1 la estamos invirtiendo gráficamente (función naranja), o dicho de otra forma, la estamos reflejando respecto el eje X.

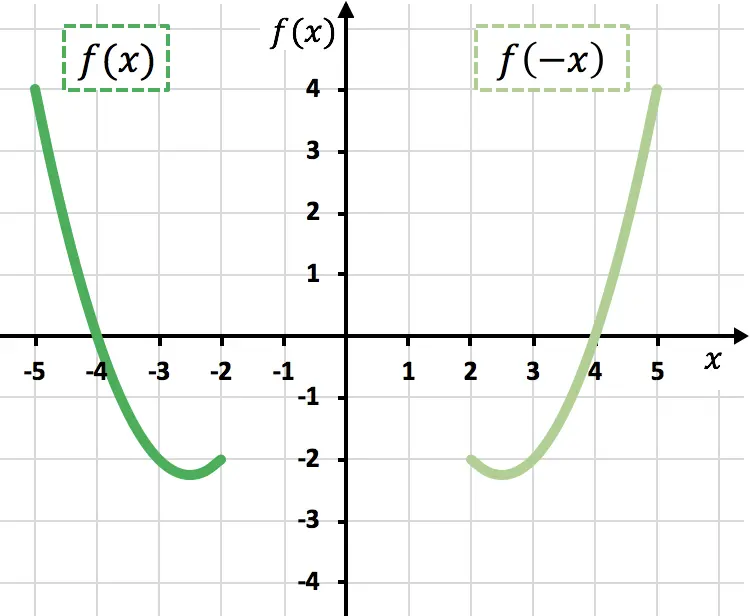
reflexion o simetria respecto el eje Y

Tal y como se aprecia en la gráfica anterior, al negar la variable x estamos reflejando la función respecto al eje Y (función verde claro).

Ejemplo de cómo reflejar una función

  • Calcula la función simétrica respecto el eje OX y la función simétrica respecto el eje OY de la siguiente función cuadrática:

f(x)=x^2-4x+6

Para encontrar la función simétrica respecto el eje X tenemos que hacer -f(x):

-f(x)=-\bigl[x^2-4x+6\bigr]

\bm{-f(x)=-x^2+4x-6}

Y para hallar la función simétrica respecto el eje Y tenemos que hacer f(-x). Por lo tanto, sustituimos donde haya una x en la función original por el término -x :

f(x)=x^2-4x+6

f(-x)=(-x)^2-4\cdot (-x)+6

f(-x)=x^2-4\cdot (-x)+6

\bm{f(-x)=x^2+4x+6}

A continuación tienes representadas tanto la función original como las funciones simétricas halladas:

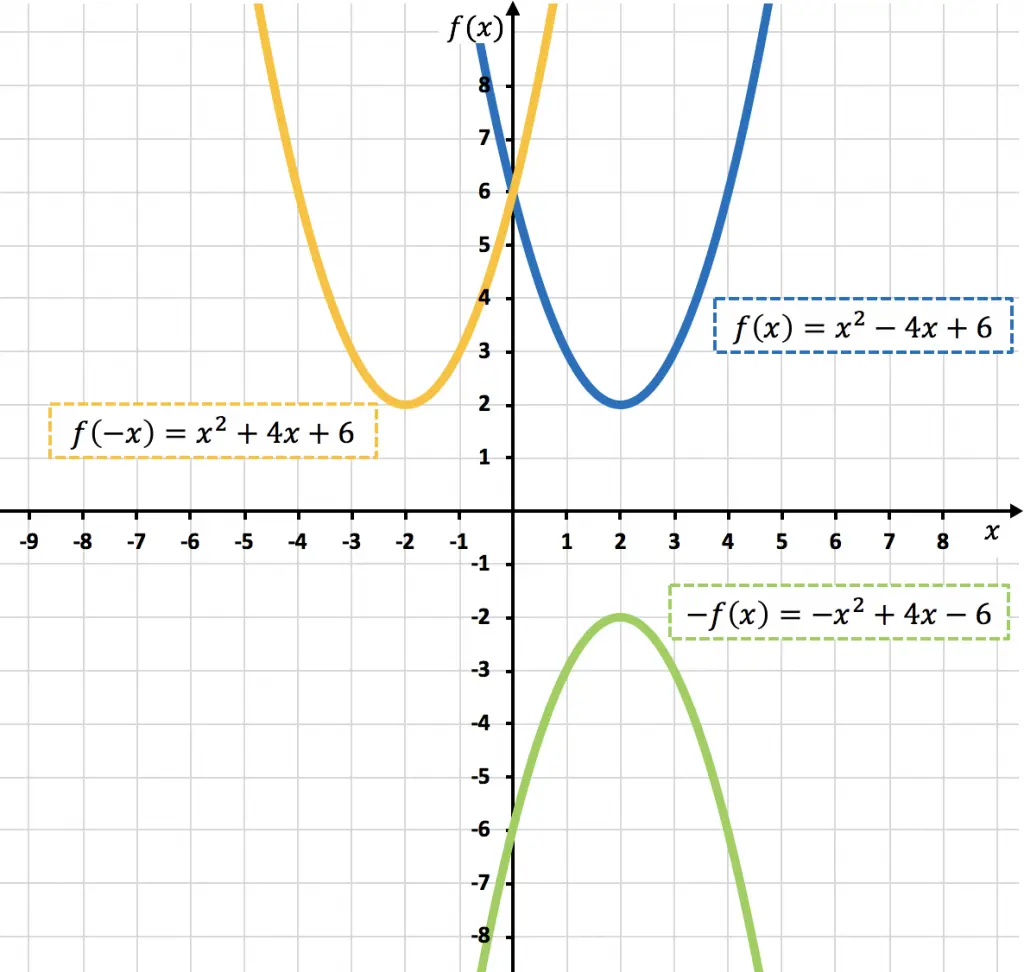
ejemplo de funciones simetricas respecto el eje x e y

Expansiones y contracciones de las funciones

Al igual que con las traslaciones, existen dos tipos de expansiones o contracciones: las verticales y las horizontales.

Expansión y contracción vertical de una función

Multiplicando toda una función por un coeficiente podemos provocar que se expanda o que se contraiga:

Para expandir (o dilatar) una función en el eje Y tenemos que multiplicarla por un número más grande que 1:

kf(x)\qquad k>1

Para contraer una función en el eje Y tenemos que multiplicarla por un número positivo más pequeño que 1:

kf(x)\qquad 0<k<1

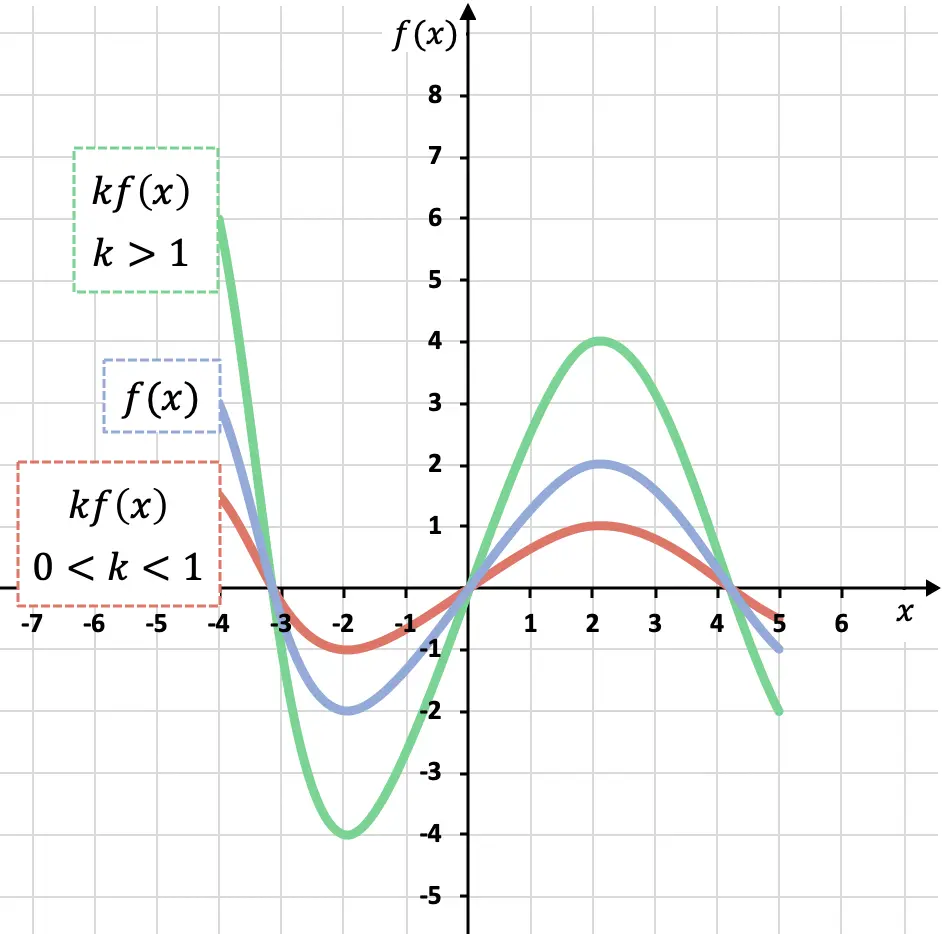
expansion y contraccion vertical de una funcion

Como puedes ver en la gráfica anterior, si multiplicamos una función por un coeficiente mayor que 1 (función verde) la estamos haciendo más grande a lo largo del eje OY, por otro lado, si multiplicamos una función por un coeficiente mayor que 0 pero menor que 1 (función roja) la estamos haciendo más pequeña a lo largo del eje OY.

Expansión y contracción horizontal de una función

En este caso, en vez de multiplicar toda la función por un coeficiente, para que una función se expanda o se contraiga a horizontalmente debemos multiplicar la variable independiente x.

Para expandir (o dilatar) una función en el eje X tenemos que multiplicar todas las x por un número entre 0 y 1:

f(kx)\qquad 0<k<1

Para contraer una función en el eje X tenemos que multiplicar todas las x por un número más grande que 1:

f(kx)\qquad k>1

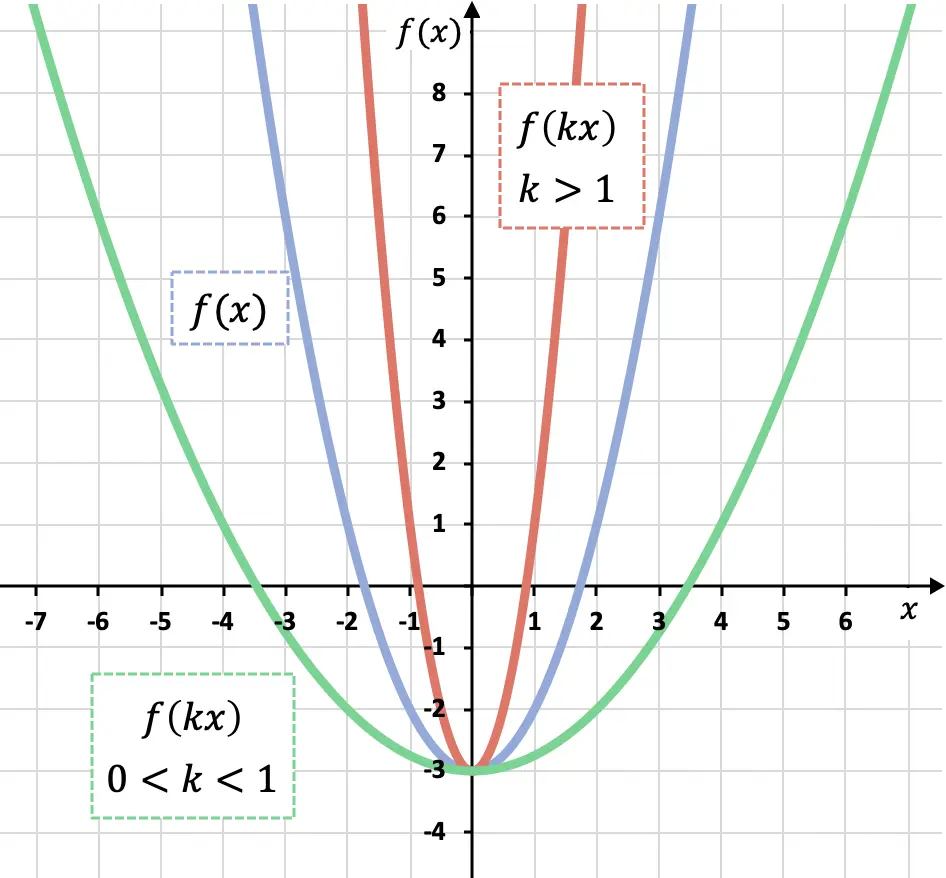
expansion o contraccion horizontal de una funcion

Como puedes ver en la gráfica anterior, si multiplicamos todas las x de una función por un coeficiente mayor que 0 pero menor que 1 (función verde) la estamos haciendo más grande a lo largo del eje OX, por otra parte, si multiplicamos una función por un coeficiente mayor que 1 (función roja) la estamos haciendo más pequeña a lo largo del eje OX.

Ejemplo de cómo expandir o contraer una función

  • Duplica verticalmente y horizontalmente la siguiente función irracional:

f(x)=\sqrt{9-x^2}

Para expandir por dos la función en el eje de las ordenadas, tenemos que multiplicar toda la función por 2:

2f(x)=2\sqrt{9-x^2}

Y para, además, expandir por dos la función en el eje de las abscisas, tenemos que multiplicar todas las x de la función por  \displaystyle \frac{1}{2}:

\displaystyle f\left(\frac{1}{2}x\right)=2\sqrt{9-\left(\frac{1}{2}x\right)^2}

Así que la función duplicada en ambos ejes de coordenadas es:

\displaystyle\bm{f(x) = 2\sqrt{9-\left(\frac{1}{2}x\right)^2}}

A continuación tienes representadas gráficamente la función original y la transformada para que puedas ver las diferencias entre ellas:

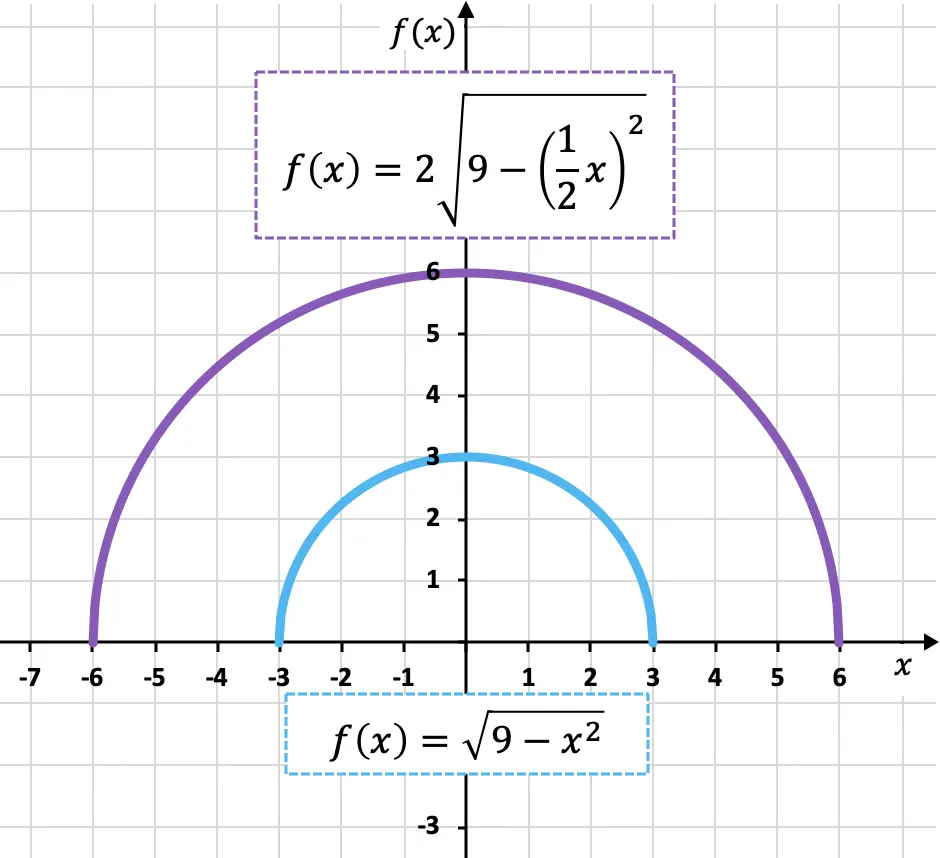
ejemplo de como expandir y contraer una funcion

Como puedes ver, la nueva función (color lila) es el doble de grande que la función original (color azul) tanto verticalmente como horizontalmente, por lo tanto, la función se ha expandido.

Ejercicios resueltos de transformaciones de funciones

Ejercicio 1

Desplaza 5 unidades hacia arriba la siguiente función de tercer grado:

f(x) = 4x^3-9x-2

Para desplazar la función 5 unidades hacia arriba debemos sumar 5 a la función:

\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}

Por tanto, la función desplazada 5 unidades hacia arriba es:

\bm{f(x) = 4x^3-9x+3}

 

Ejercicio 2

Halla la función simétrica respecto el eje Y de la siguiente función cuadrática:

f(x) = 2x^2-3x+6

Para hallar la función simétrica respecto el eje Y debemos calcular f(-x) , es decir, tenemos que sustituir x por -x en la función:

f(-x) = 2(-x)^2-3\cdot (-x)+6

f(-x) = 2x^2+3x+6

De manera que la función simétrica respecto el eje OY es:

\bm{f(x) = 2x^2+3x+6}

 

Ejercicio 3

Realiza la compresión horizontal de la siguiente función a un tercio de su representación:

f(x) = x^3-4x^2-5x+1

Para contraer una función a través del eje X (horizontalmente) tenemos que multiplicar todas las x por un número más grande que 1. En este caso queremos reducir la función a una tercera parte, por lo que debemos multiplicar las x por 3:

f(3x) = (3x)^3-4(3x)^2-5(3x)+1

f(3x) = 27x^3-4\cdot 9 x^2-15x+1

f(3x) = 27x^3-36 x^2-15x+1

Así que la función contraída es:

\bm{f(x) = 27x^3-36 x^2-15x+1}

 

Ejercicio 4

Calcula la función simétrica respecto el eje OX de la siguiente función trasladada 4 unidades a la derecha:

f(x) = 3x^3-x^2+5x+8

Antes de calcular la función simétrica, primero debemos trasladar la función 4 unidades a la derecha, por tanto:

f(x-4) = 3(x-4)^3-(x-4)^2+5(x-4)+8

f(x-4) = 3(x-4)^3-(x-4)^2+5x-20+8

f(x-4) = 3(x-4)^3-(x-4)^2+5x-12

Y una vez hemos desplazado la función, calculamos la función simétrica respecto el eje X. Para ello, debemos negar la función obtenida:

\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]

-f(x) = -3(x-4)^3+(x-4)^2-5x+12

En definitiva, la función tras haber aplicado todas las operaciones elementales queda:

\bm{f(x) =-3(x-4)^3+(x-4)^2-5x+12}

 

Ejercicio 5

Desplaza 2 unidades a la izquierda la siguiente función y luego expándela verticalmente con un factor de 4:

f(x) = x^4-5x^3-x-3

Primero trasladamos la función dos unidades a la izquierda:

f(x+2) = (x+2)^4-5(x+2)^3-(x+2)-3

f(x-4) = (x+2)^4-5(x+2)^3-x-2-3

f(x-4) = (x+2)^4-5(x+2)^3-x-5

Y luego hacemos la expansión de la función a lo largo del eje Y con un factor de 4:

4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]

f(x) = 4(x+2)^4-20(x+2)^3-4x-20

En conclusión, la función tras haber aplicado todas las transformaciones elementales queda:

\bm{f(x) =4(x+2)^4-20(x+2)^3-4x-20}

 

Ejercicio 6

A partir de la función  f(x)=x, determina cuál de la representaciones que hay en la gráfica corresponde a la función f(x)=x-3 .

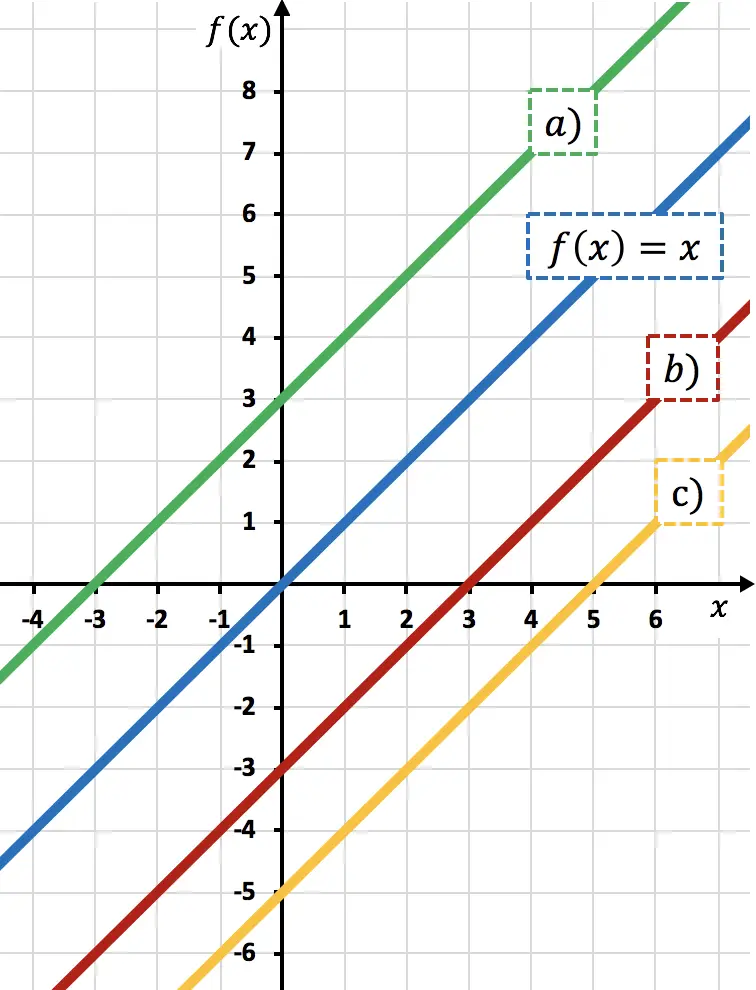
ejercicios resueltos paso a paso de transformaciones de funciones

La función f(x)=x-3 es la función f(x)=x desplazada 3 unidades hacia abajo. Ya que al restar un número a una función se está desplazando la función hacia abajo.

Por tanto, la representación de  f(x)=x-3 corresponde a la recta b), porque está desplazada 3 unidades hacia abajo respecto f(x)=x .

Esto se puede ver mirando al eje vertical: cuando f(x)=x pasa por el 0, la recta roja pasa por -3, así que está desplazada 3 unidades hacia abajo.

 

Ejercicio 7

A partir de la función  f(x)=x^2+2, determina qué parábola es la representación de la función  f(x)=(x-6)^2+2 .

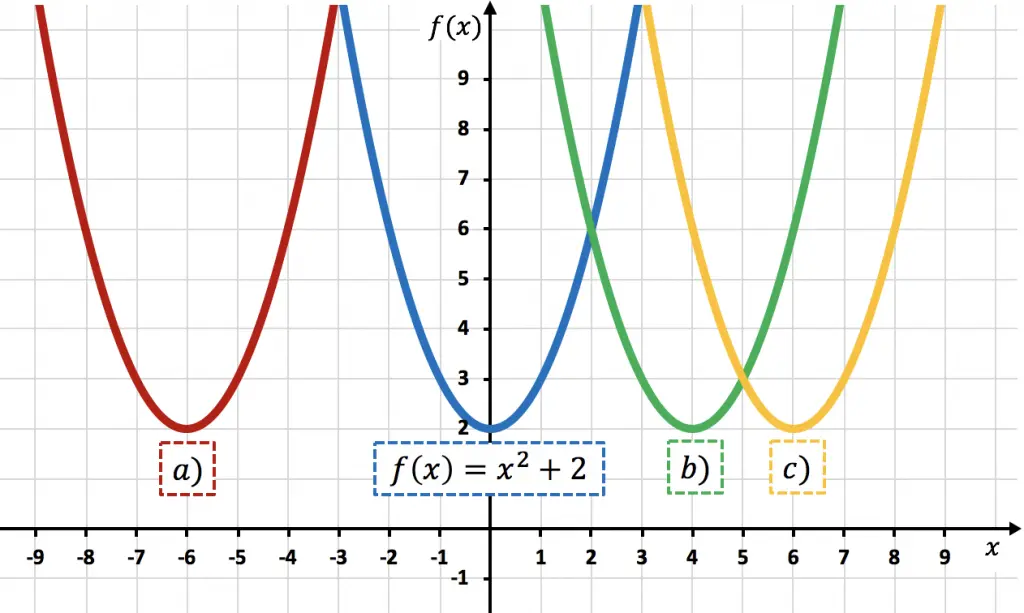
problemas resueltos de transformaciones de funciones

La función f(x)=(x-6)^2+2 es la función f(x)=x^2+2 desplazada 6 unidades hacia la derecha. Lo podemos comprobar calculando f(x-6):

f(x)=x^2+2

f(x-6)=(x-6)^2+2

Por tanto, la representación de f(x)=(x-6)^2+2 corresponde a la parábola c), porque está desplazada 6 unidades hacia la derecha respecto f(x)=x^2+2 .

Esto se puede ver mirando a los vértices de las parábolas: la distancia entre el vértice de la parábola f(x)=x^2+2 y el vértice de la parábola c) es de 6 unidades, así que esta última está desplazada 6 unidades hacia la derecha respecto la primera.

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *