Aquí te explicamos qué es un punto de inflexión de una función y cómo hallar todos los puntos de inflexión de una función. Además, encontrarás ejercicios resueltos paso a paso de la curvatura y de puntos de inflexión de una función
Índice
¿Qué son los puntos de inflexión de una función?
Los puntos de inflexión de una función son aquellos puntos en los que la gráfica de la función cambia de curvatura, es decir, en un punto de inflexión una función pasa de ser cóncava a ser convexa o viceversa.
Cómo saber si una función tiene un punto de inflexión
Vista la definición de punto de inflexión, vamos a ver cómo se puede saber si un determinado punto es un punto de inflexión de la función.
Una función tiene un punto de inflexión en los puntos que anulan su segunda derivada y su tercera derivada es diferente de cero.
A modo de ejemplo, vamos a calcular los puntos de inflexión de la siguiente función de tercer grado:
Primero de todo, calculamos la segunda y la tercera derivada de la función:
Ahora igualamos la segunda derivada a 0 y resolvemos la ecuación resultante:
Entonces, el punto x=0 será un punto de inflexión de la función si la tercera derivada es distinta de cero en ese punto. En nuestro caso, la tercera derivada siempre es igual a 6.
Por lo tanto, x=0 es un punto de inflexión de la función.
Cómo estudiar la curvatura y hallar los puntos de inflexión de una función
Acabamos de ver un método para encontrar los puntos de inflexión. Sin embargo, normalmente se suele estudiar la curvatura de una función, es decir, determinar la concavidad y la convexidad de una función, y a partir de aquí calcular los puntos de inflexión.
Para hallar los puntos de inflexión de una función a través de su curvatura se deben hacer los siguientes pasos:
- Hallar los puntos que no pertenecen al dominio de la función.
- Calcular la primera derivada y la segunda derivada de la función.
- Hallar las raíces de la segunda derivada, es decir, calcular los puntos que anulan la segunda derivada resolviendo
.
- Hacer intervalos con las raíces de la derivada y los puntos que no pertenecen al dominio de la función.
- Calcular el valor de la segunda derivada en un punto de cada intervalo.
- El signo de la segunda derivada determina la concavidad o convexidad de la función en ese intervalo:
- Si la segunda derivada de la función es positiva, la función es convexa en ese intervalo.
- Si la segunda derivada de la función es negativa, la función es cóncava en ese intervalo.
- Los puntos de inflexión son aquellos puntos en los que la función pasa de ser convexa a ser cóncava o viceversa.
Para que veas cómo se calculan los puntos de inflexión de una función utilizando este procedimiento, vamos a resolver un ejemplo paso a paso a cotinuación:
- Estudia la curvatura y halla los puntos de inflexión de la siguiente función polinómica:
Lo primero que debemos hacer es calcular el dominio de la función. Se trata de una función polinómica, por lo que el dominio de la función son todos los números reales, es decir, se trata de una función continua:
Una vez hemos calculado el dominio de la función, debemos estudiar en qué puntos se cumple .
Así que primero calculamos la primera derivada de la función:
A continuación calculamos la segunda derivada de la función:
Y ahora igualamos la segunda derivada a 0 y resolvemos la ecuación:
Una vez hemos calculado el dominio de la función y , representamos en la recta numérica todos los puntos críticos encontrados:
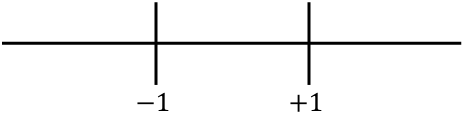
Y ahora evaluamos el signo de la segunda derivada en cada intervalo, para saber si la función es cóncava o convexa. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos críticos) y miramos qué signo tiene la segunda derivada en ese punto:

Si la segunda derivada es positiva significa que la función es convexa , y si la segunda derivada es negativa significa que la función es cóncava
. Por tanto, los intervalos de concavidad y convexidad de la función son:
Convexa :
Cóncava :
Además, en x=-1 la función pasa de ser convexa a ser cóncava, así que x=-1 es un punto de inflexión de la función. Y en x=1 la función pasa de ser cóncava a ser convexa, por lo que x=1 también es un punto de inflexión de la función.
Por último, sustituimos los puntos encontrados en la función original para hallar la coordenada Y de los puntos de inflexión:
Así que los puntos de inflexión de la función son:
Puntos de inflexión: y
Abajo puedes ver la representación gráfica de la función estudiada:
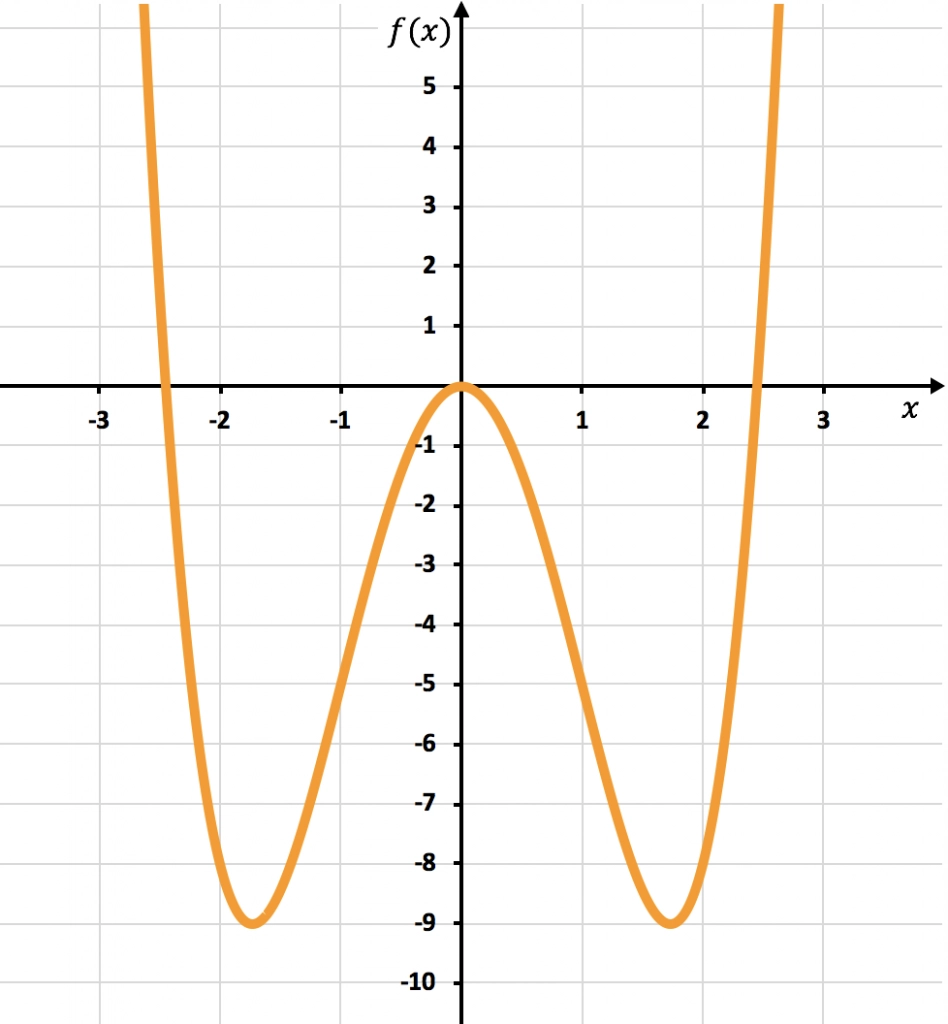
Como puedes ver en el gráfico, la función pasa de ser convexa a ser cóncava
en el punto
ya que cambia su curvatura. Y, por otro lado, la función pasa de ser cóncava
a ser convexa
en el punto
.
Ejercicios resueltos de puntos de inflexión
Ejercicio 1
Calcula los intervalos de concavidad y convexidad y los puntos de inflexión de la siguiente función exponencial:
Lo primero que debemos hacer es calcular el dominio de la función. La función está compuesta por una función polinómica (x), cuyo dominio son todos los números reales, y por una función exponencial (ex), cuyo dominio también son todos los números reales. Por tanto, el dominio de la función son todos los números reales:
Ahora calculamos la derivada de la función. En este caso la función está compuesta por el producto de dos funciones, por tanto, para derivar la función debemos aplicar la fórmula de la derivada de un producto:
A continuación calculamos la segunda derivada de la función:
Igualamos la segunda derivada a 0 y resolvemos la ecuación:
Extraemos factor común:
Para que la multiplicación valga 0, uno de los dos elementos de la multiplicación tiene que ser cero. Por lo tanto, igualamos cada factor a 0:
Un número elevado a otro nunca puede dar 0. Por tanto, la ecuación no tiene solución.
Representamos en la recta todos los puntos singulares obtenidos:
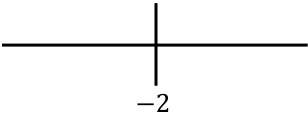
Y ahora evaluamos el signo de la segunda derivada en cada intervalo para saber si la función es cóncava o convexa. Para ello, cogemos un punto de dentro de cada intervalo y miramos qué signo tiene la segunda derivada en ese punto:

Si la segunda derivada es positiva significa que la función es convexa , y si la segunda derivada es negativa significa que la función es cóncava
. Por tanto, los intervalos de concavidad y convexidad son:
Convexa :
Cóncava :
Además, la función pasa de ser cóncava a ser convexa en x=-2, así que x=-2 es un punto de inflexión de la función.
Por último, sustituimos el punto de inflexión encontrado en la función original para hallar la coordenada Y del punto:
En conclusión, el único punto de inflexión de la función son:
Puntos de inflexión:
Ejercicio 2
Estudia los intervalos de concavidad y convexidad y halla los puntos de inflexión de la siguiente función racional:
Primero tenemos que calcular el dominio de la función. Como se trata de una función racional, igualamos a cero el denominador para ver qué números no pertenecen al dominio de la función:
Esto significa que cuando x sea -2 o +2, el denominador será 0. Y, en consecuencia, la función no existirá. Así que el domino de la función son todos los números excepto x=-2 y x=+2.
En segundo lugar, calculamos la primera derivada de la función:
Y luego resolvemos la segunda derivada:
Todos los términos están multiplicados por . Así que podemos simplificar la fracción:
Ahora calculamos las raíces de la segunda derivada de la función:
El término está dividiendo a todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:
Extraemos factor común:
Para que la multiplicación valga 0, uno de los dos elementos de la multiplicación tiene que ser zero. Por lo tanto, igualamos cada factor a 0:
no tiene solución, ya que no existe la raíz negativa de un número real.
Ahora representamos en la recta todos los puntos críticos obtenidos, es decir, los puntos que no pertenecen al dominio (x=-2 y x=+2) y los que anulan la segunda derivada (x=0):

Y evaluamos el signo de la segunda derivada en cada intervalo, para saber si la función es cóncava o convexa. De manera que cogemos un punto de dentro de cada intervalo y miramos qué signo tiene la segunda derivada en ese punto:

Si la segunda derivada es positiva significa que la función es convexa , y si la segunda derivada es negativa significa que la función es cóncava
. Por tanto, los intervalos de concavidad y convexidad son:
Convexa :
Cóncava :
La función cambia de curvatura en tres puntos, por lo tanto, la función racional en principio tendría tres puntos de inflexión, que son x=-2, x=0 y x=2. Sin embargo, aunque haya un cambio de curvatura en x=-2 y en x=+2, estos no son puntos de inflexión porque no pertenecen al dominio de la función. En cambio, en x=0 hay un cambio de curvatura y sí que pertenece a la función, de modo que x=0 es el único punto de inflexión de la función.
Ahora solo nos queda calcular la coordenada Y del punto de inflexión:
En definitiva, el único punto de inflexión de la función racional es el origen de coordenadas:
Puntos de inflexión:
Ejercicio 3
Sabemos que la función pasa por el punto
, tiene un extremo relativo en
, y un punto de inflexión en
. A partir de esta información, calcula los valores de los parámetros
y
.
Que la función tenga un punto de inflexión en significa que
. Por tanto, calculamos la segunda derivada de la función en
y la igualamos a 0:
Y resolvemos la ecuación obtenida para hallar el valor del parámetro a:
De manera que la función será:
A parte, la función tiene un extremo en , lo que significa que
. Por tanto, calculamos la primera derivada de la función en
y la igualamos a 0:
Y resolvemos la ecuación obtenida para hallar el valor de la incógnita b:
De manera que la función será:
Por otro lado, nos dicen que la función pasa por el punto (3,1). Es decir, . Por tanto, podemos aplicar esta condición para hallar el valor del parámetro c:
Y resolvemos la ecuación obtenida para hallar el valor de
De manera que la función será:

En el ultimo ej la c es igual a 0, no 1.
Hola Maney, el resultado está ben, c debe ser igual a 1 para que se cumplan las condiciones.