Monotonía de una función: crecimiento y decrecimiento

En este post te explicamos cómo saber la monotonía de una función, es decir, cómo hallar los intervalos de crecimiento y decrecimiento de una función. Además, podrás practicar con ejercicios resueltos paso a paso del crecimiento y decrecimiento de una función.

¿Qué es la monotonía de una función?

Una función es monótona en un intervalo si conserva el orden dado. Existen cinco tipos de monotonía:

  • Función monótona creciente: cuando el valor de la función en un punto siempre es igual o mayor al valor de la función en un punto anterior.

    • f(x)\leq f(y) \qquad x<y

  • Función monótona decreciente: cuando el valor de la función en un punto siempre es igual o menor al valor de la función en un punto anterior.

    • f(x)\geq f(y) \qquad x<y

  • Función estrictamente monótona creciente: cuando el valor de la función en un punto siempre es mayor al valor de la función en un punto anterior.

    • f(x)< f(y) \qquad x<y

  • Función estrictamente monótona decreciente: cuando el valor de la función en un punto siempre es menor al valor de la función en un punto anterior.

    • f(x)>f(y) \qquad x<y

  • Función constante cuando el valor de la función en un punto siempre es igual al valor de la función en un punto anterior.

    • f(x)=f(y) \qquad x<y

Ten en cuenta que una función constante es al mismo tiempo una función monótona creciente y monótona decreciente, ya que también cumple con sus definiciones.

Entonces, diremos que una función es monótona cuando satisface alguna de las definiciones anteriores en todo su dominio.

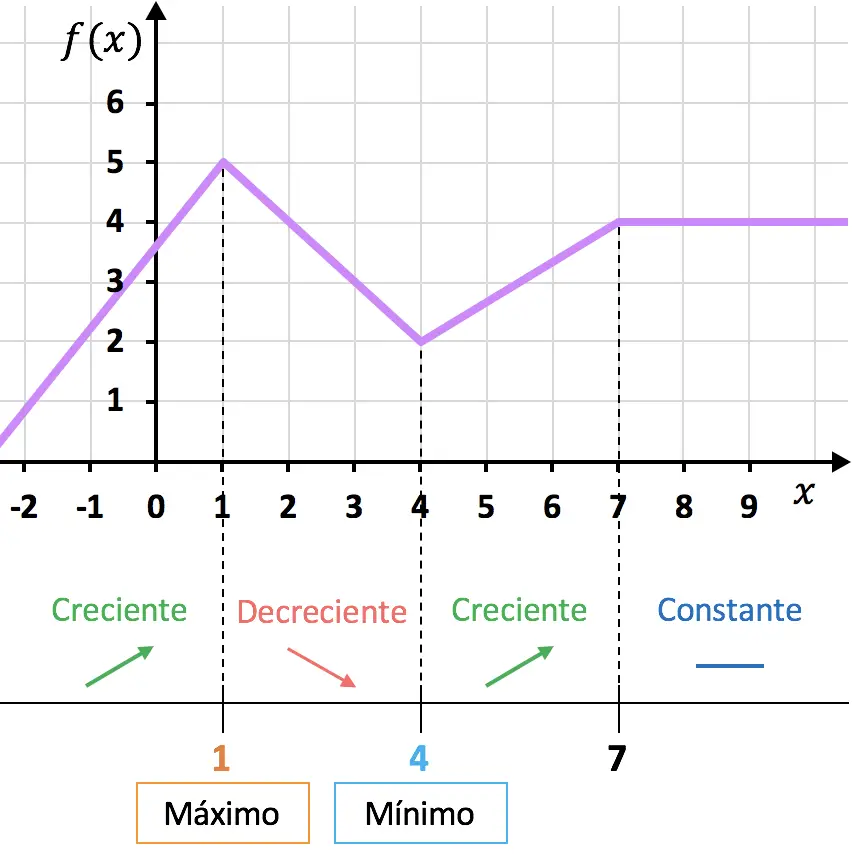
monotonia de una funcion crecimiento y decrecimiento grafica

Como puedes ver en la gráfica anterior, la función es creciente cuando su representación va «hacia arriba», la función es decreciente cuando va «hacia abajo», y la función es constante cuando se mantiene igual.

Por otro lado, en el punto en el que la función pasar de ser creciente a ser decreciente o viceversa, decimos que ese punto es un extremo relativo:

  • Si la función pasa de ser creciente a ser decreciente, el punto es un máximo relativo.
  • Si la función pasa de ser decreciente a ser creciente, el punto es un mínimo relativo.

Cómo estudiar la monotonía de una función

Para estudiar la monotonía de una función, es decir, los intervalos de crecimiento y decrecimiento de una función, debemos hacer los siguientes pasos:

  1. Hallar los puntos que no pertenecen al dominio de la función.
  2. Calcular la derivada de la función.
  3. Hallar las raíces de la derivada, es decir, calcular los puntos que anulan la derivada resolviendo f'(x)=0.
  4. Hacer intervalos con las raíces de la derivada y los puntos que no pertenecen al dominio de la función.
  5. Calcular el valor de la derivada en un punto de cada intervalo.
  6. El signo de la derivada determina el crecimiento o decrecimiento de la función en ese intervalo:
    • Si la derivada de la función es positiva, la función es creciente en ese intervalo.
    • Si la derivada de la función es negativa, la función es decreciente en ese intervalo.

Ejemplo de cómo hallar la monotonía de una función

Vista la teoría de la monotonía de una función, a continuación vamos a resolver un ejemplo paso a paso para que entiendas perfectamente cómo se estudia la monotonía de una función

  • Analiza la monotonía de la siguiente función racional:

f(x)=\cfrac{3}{x^2-4}

Lo primero que debemos hacer es calcular el dominio de la función. Se trata de una función racional, por tanto, debemos igualar a 0 el denominador para ver qué números no pertenecen al dominio de la función:

x^2-4=0

x^2=4

x=\pm 2

De manera que cuando x sea +2 o -2, el denominador será 0. Y, en consecuencia, la función no existirá. Así que el domino de la función son todos los números excepto x=±2.

\text{Dom } f= \mathbb{R}-\{+2, -2 \}

Una vez hemos calculado el dominio de la función, debemos estudiar en qué puntos se anula la primera derivada de la función.

Así que primero calculamos la derivada de la función aplicando la fórmula de la derivada de una división:

f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) - 3\cdot 2x}{\left(x^2-4\right)^2}

f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}

Y ahora igualamos la derivada a 0 y resolvemos la ecuación:

f'(x)=0

\cfrac{-6x}{\left(x^2-4\right)^2}=0

El término \left(x^2-4\right)^2} está dividiendo a todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:

-6x=0\cdot \left(x^2-4\right)^2

-6x=0

x=\cfrac{0}{-6}

x=0

Una vez hemos calculado el dominio de la función y f'(x)=0, representamos en la recta todos los puntos críticos encontrados:

Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece en cada intervalo. Para ello, cogemos un punto de dentro de cada intervalo (nunca los puntos críticos) y miramos qué signo tiene la derivada en ese punto:

f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}

f'(-3) = \cfrac{-6\cdot(-3)}{\left((-3)^2-4\right)^2} = \cfrac{+18}{+25} = +0,72 \ \rightarrow \ \bm{+}

f'(-1) = \cfrac{-6\cdot(-1)}{\left((-1)^2-4\right)^2} = \cfrac{+6}{+9} = +0,67 \ \rightarrow \ \bm{+}

f'(1) = \cfrac{-6\cdot 1}{\left(1^2-4\right)^2} = \cfrac{-6}{+9} = -0,67 \ \rightarrow \ \bm{-}

f'(3) = \cfrac{-6\cdot3}{\left(3^2-4\right)^2} = \cfrac{-18}{+25} = - 0,72 \ \rightarrow \ \bm{-}

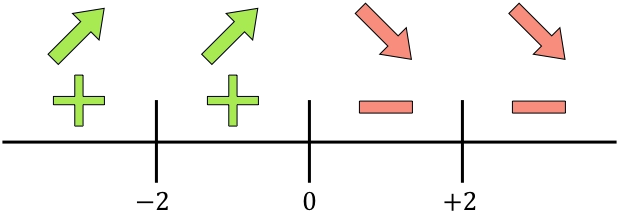
Por último, deducimos los intervalos de decrecimiento y crecimiento de la función. Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. De modo que los intervalos de crecimiento y decrecimiento de la función son:

Crecimiento: \bm{(-\infty, -2)\cup (-2,0)}

Decrecimiento: \bm{(0,2)\cup (2,+\infty)}

Nota: aunque el intervalo (-∞,-2) tenga el mismo signo que el intervalo (-2,0), se tiene que expresar los intervalos con el signo U:

(-\infty, -2)\cup (-2,0) ✅

Y nunca escribirlo así: (-\infty,0) ❌. Porque la función no existe en el punto -2 y, por tanto, ese punto no se debe incluir en el intervalo.

Ejercicios resueltos de la monotonía de una función

Ejercicio 1

Estudia el crecimiento y decrecimiento de la siguiente función polinómica:

\displaystyle f(x)=x^3-6x^2+9x

Es una función polinómica, así que el dominio de la función son todos los números reales:

\text{Dom } f= \mathbb{R}

Una vez hemos sabemos el dominio de la función, debemos estudiar en qué puntos se cumple f'(x)=0. Por lo que derivamos la función de tercer grado:

f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9

Y ahora igualamos la derivada a 0 y resolvemos la ecuación de segundo grado utilizando la fórmula general:

f'(x)= 0

3x^2-12x+9=0

\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(-12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108}}{6} =\cfrac{12 \pm 6}{6}=\begin{cases} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 - 6}{6}=1 \end{cases} \end{aligned}

Una vez hemos calculado el dominio de la función y f'(x)=0, representamos en la recta numérica todos los puntos singulares encontrados:

Y, finalmente, determinamos el signo de la derivada en cada intervalo. Para ello, cogemos un punto de dentro de cada intervalo y miramos qué signo tiene la derivada en ese punto:

f'(0)=3\cdot 0^2-12\cdot0+9 =+9 \ \rightarrow \ \bm{+}

f'(2)=3\cdot2^2-12\cdot2+9 =-3 \ \rightarrow \ \bm{-}

f'(4)=3\cdot4^2-12\cdot4+9 =+9 \ \rightarrow \ \bm{+}

La función crecerá en los intervalos que su derivada sea positiva y, por contra, la función decrecerá en los intervalos que su derivada sea negativa. Por tanto:

Crecimiento: \bm{(-\infty, 1)\cup (3,+\infty)}

Decrecimiento: \bm{(1,3)}

 

Ejercicio 2

Estudia la monotonía de la siguiente función racional:

\displaystyle f(x)=\frac{5}{x^2-9}

En primer lugar, debemos encontrar el dominio de la función. Así que igualamos el denominador a cero y resolvemos la ecuación cuadrática resultante:

x^2-9 = 0

x^2 = 9

x = \pm 3

Por tanto, cuando x sea igual a +3 o -3, el denominador será 0 y la función no existirá.

\text{Dom } f= \mathbb{R}-\{+3, -3 \}

Una vez hemos calculado el dominio de la función, debemos estudiar en qué puntos la derivada es nula. Por lo que derivamos la función:

f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) - 5\cdot (2x)}{\left(x^2-9\right)^2}

f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}

Ahora igualamos la derivada a 0 y resolvemos la ecuación:

f'(x)= 0

\cfrac{-10x}{\left(x^2-9\right)^2}=0

-10x=0\cdot \left(x^2-9\right)^2

-10x= 0

x= \cfrac{0}{-10}

x=0

Entonces, representamos en la recta todos los puntos singulares encontrados:

Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos singulares) y miramos qué signo tiene la derivada en ese punto:

f'(-4)= \cfrac{-10(-4)}{\left((-4)^2-9\right)^2}= \cfrac{+40}{+49} =+0,82 \ \rightarrow \ \bm{+}

f'(-1)= \cfrac{-10(-1)}{\left((-1)^2-9\right)^2}= \cfrac{+10}{+64} = +0,16 \ \rightarrow \ \bm{+}

f'(1)= \cfrac{-10\cdot 1}{\left(1^2-9\right)^2}= \cfrac{-10}{+64} = -0,16 \ \rightarrow \ \bm{-}

f'(4)= \cfrac{-10\cdot 4}{\left(4^2-9\right)^2}= \cfrac{-40}{+7} =-0,82 \ \rightarrow \ \bm{-}

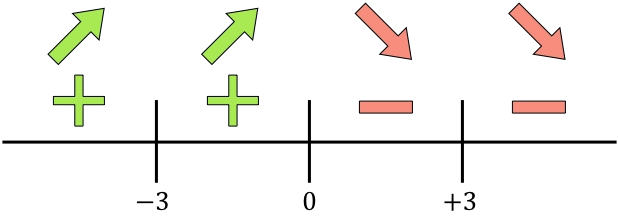
Si la derivada es positiva significa que la función crece, en cambio, si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento de la función racional son:

Crecimiento: \bm{(-\infty, -3)\cup (-3,0)}

Decrecimiento: \bm{(0,3)\cup (3,+\infty)}

 

Ejercicio 3

Calcula la monotonía de la siguiente función logarítmica:

\displaystyle f(x)=\ln\left(x^2+1\right)

Primero tenemos que estudiar el dominio de la función logarítmica. Al ser un logaritmo, debemos mirar cuándo su argumento es más grande que 0, ya que no existe ni el logaritmo natural de un número negativo ni de 0:

x^2+1> 0

En este caso la función cuadrática x2+1 siempre será positiva, porque el cuadrado de un número siempre será positivo. Por tanto, el dominio de la función serán todos los números reales:

\text{Dom } f= \mathbb{R}

Una vez hemos calculado el dominio de la función, tenemos que calcular los ceros (o raíces) de la derivada de la función. Por lo que calculamos la derivada de la función:

f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)

f'(x)= \cfrac{2x}{x^2+1}

Ahora igualamos la derivada a 0 y resolvemos la ecuación:

f'(x)= 0

\cfrac{2x}{x^2+1}=0

2x=0\cdot \left(x^2+1\right)

2x= 0

x= \cfrac{0}{2}

x=0

Una vez hemos calculado el dominio de la función y las raíces de la primera derivada de la función, representamos en la recta todos los puntos críticos hallados, que en este caso solamente es el cero:

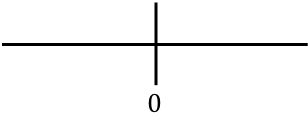
Evaluamos el signo de la derivada en cada intervalo para saber si la función crece o decrece:

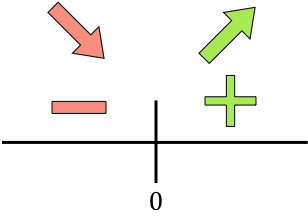
f'(-1)= \cfrac{2\cdot(-1)}{(-1)^2+1}= \cfrac{-2}{+2} = -1 \ \rightarrow \ \bm{-}

f'(1)= \cfrac{2\cdot1}{1^2+1}= \cfrac{+2}{+2} = +1 \ \rightarrow \ \bm{+}

Si la derivada es positiva significa que la función crece, pero si la derivada es negativa significa que la función decrece. En conclusión, los intervalos de crecimiento y decrecimiento de la función son:

Crecimiento: \bm{(0,+\infty)}

Decrecimiento: \bm{(-\infty,0)}

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *