Límites al infinito

Aquí encontrarás cómo resolver todos los tipos de límites al infinito: funciones polinómicas, racionales, exponenciales, con raíces, indeterminaciones con infinito… Además, podrás practicar con 25 ejercicios resueltos paso a paso de límites cuando x tiende a infinito.

Límite de una función cuando x tiende a infinito

El límite de una función cuando x tiende a infinito, ya sea positivo o negativo, puede ser un valor real, más infinito, menos infinito o no existir. Para resolver límites al infinito, se debe sustituir la x por infinito.

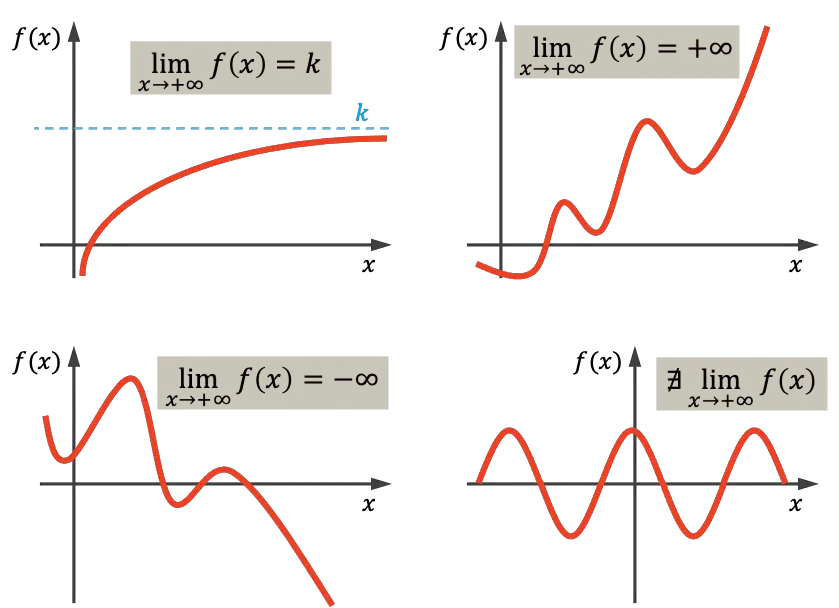
limites al infinito

Como puedes ver en el primer gráfico, la función representada tiende al valor real k al infinito, porque se va acercando a k a medida que x va creciendo. La función de arriba a la derecha tiende al más infinito cuando x tiende a infinito, ya que crece indefinidamente al aumentar de valor la x. En cambio, la gráfica de abajo a la izquierda decrece sin parar y por eso tiende a menos infinito. Finalmente, la última función es periódica y no tiende a ningún valor, por lo tanto, no existe el límite en el infinito en este caso.

Cómo resolver límites al infinito

Para resolver un límite al infinito en funciones polinómicas, debemos sustituir la x por el infinito solamente en el término de mayor grado de la función.

Por ejemplo, fíjate en el siguiente cálculo de un límite al infinito donde únicamente sustituimos el infinito en el monomio de mayor grado:

\displaystyle \lim_{x \to +\infty}(3x^2-4x+6) = 3(+\infty)^2 = \bm{+\infty}

Como puedes ver en el ejemplo, +∞ elevado al cuadrado da +∞, ya que un número muy grande (+∞) elevado a la 2 seguirá dando como resultado un número muy grande (+∞).

Y sucede lo mismo con la multiplicación: si multiplicas un número muy grande (+∞) seguirá dando como resultado un número muy grande (+∞). Por ejemplo: 3\cdot (+\infty)= +\infty.

Atención: para calcular límites en el infinito es importante que tengas en cuenta lo siguiente:

→ Un número negativo elevado a un exponente par da positivo. Por tanto, menos infinito elevado a un exponente par da más infinito:

(-\infty)^2 = +\infty

→ Un número negativo elevado a un exponente impar da negativo. Por tanto, menos infinito elevado a un exponente impar es menos infinito:

(-\infty)^3 = -\infty

→ La multiplicación de un número negativo cambia el signo del infinito:

-2(+\infty) = - \infty

→ Cualquier número dividido entre \pm \infty da como resultado 0:

\cfrac{5}{\infty} = 0

Ejemplos de límites al infinito

Para que puedas ver cómo se resuelven los límites al infinito en polinomios, a continuación tienes resueltos varios límites de este tipo:

\begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}

Límites al infinito indeterminados

Los límites en el infinito no siempre serán tan fáciles de calcular, ya que en ocasiones obtendremos la indeterminación infinito entre infinito o la indeterminación infinito menos infinito.

\cfrac{\infty}{\infty}\qquad \qquad \infty-\infty

Cuando obtenemos estos tipos de indeterminaciones (o formas indeterminadas) no podemos saber el resultado directamente, sino que debemos hacer un procedimiento previo para hallar el valor de límite. A continuación vamos a ver cómo se resuelven los límites indeterminados al infinito.

Indeterminación infinito entre infinito

Para hallar el resultado de la indeterminación infinito dividido entre infinito tenemos que comparar el grado del numerador y el grado denominador de la fracción:

  1. Si el grado del polinomio del numerador es menor que el grado del polinomio del denominador, la indeterminación infinto partido por infinito es igual a cero.
  2. Si el grado del polinomio del numerador es equivalente al grado del polinomio del denominador, la indeterminación infinito sobre infinito es el cociente de los coeficientes principales de los dos polinomios.
  3. Si el grado del polinomio del numerador es mayor que el grado del polinomio del denominador, la indeterminación infinito entre infinto da más o menos infinito (el signo depende de los términos principales de ambos polinomios).

\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex] \cfrac{a_n}{b_n} & \text{si} & r=s \\[5ex] \pm \infty & \text{si} & r>s \end{array}\right.

Por ejemplo, en el siguiente límite, el polinomio del numerador es de segundo grado, mientras que el polinomio del denominador es de tercer grado, por lo tanto, la solución del límite es 0.

\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}

Fíjate en este otro ejemplo, en el que los dos polinomios de la función racional son de segundo grado, por lo que tenemos que dividir los coeficientes de los términos de mayor grado para calcular el límite en el infinito.

\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}

Finalmente, en el siguiente límite la función del numerador tiene mayor grado que la del denominador, por lo que la indeterminación infinito sobre infinito da infinito. Además, del numerador se obtiene un infinito positivo, pero del denominador un infinito negativo, así que el resultado del límite es negativo (positivo entre negativo da negativo).

\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}

Indeterminación infinito entre infinito con raíces

Por otro lado, el grado de una función irracional (función con raíces) es el cociente entre el grado del término principal y el índice del radical.

\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}

Por lo tanto, si el límite de una función con raíces da la indeterminación infinito entre infinito, tenemos que aplicar las mismas reglas explicadas arriba de los grados del numerador y del denominador, pero teniendo en cuenta que el grado de un polinomio con raíces se calcula diferente.

Fíjate en el siguiente ejemplo del límite al infinito de una función con radicales:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}

El grado del numerador es 2, y el grado del denominador es 4 (8/2=4), por lo tanto, el límite da 0 porque el grado del numerador es menor que el grado del denominador.

Indeterminación infinito entre infinito con funciones exponenciales

El crecimiento de una función exponencial es mucho más grande que el crecimiento de una función polinómica, así que debemos considerar que el grado de una función exponencial es mayor que el grado de una función polinómica.

\text{exponencial}>\text{polinomio}

Por lo tanto, si la indeterminación infinito partido por infinito resulta de un límite con funciones exponenciales, simplemente debemos aplicar las mismas reglas explicas de los grados del numerador y del denominador, pero teniendo en cuenta que una función exponencial es de mayor orden que un polinomio.

Además, si tenemos funciones exponenciales en el numerador y en el denominador de la división, la función exponencial cuya base sea más grande será la que tendrá mayor orden.

\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}

En este ejemplo, el denominador está formado por una función exponencial, por lo que es de mayor orden que el numerador. En consecuencia, la forma indeterminada infinito entre infinito da 0.

Indeterminación infinito menos infinito

La resolución de la indeterminación infinito menos infinito depende de si la función tiene fracciones o raíces. Así que vamos a ver cómo solucionar este tipo de indeterminación para estos dos casos distintos.

Indeterminación infinito menos infinito con fracciones

Cuando la indeterminación infinito menos infinito se produce en una suma o resta de fracciones algebraicas, primero tenemos que hacer la suma o la resta de las fracciones y luego calcular el límite.

Veamos cómo calcular la indeterminación infinito menos infinito en una función con fracciones resolviendo un ejemplo paso a paso:

\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)

Primero intentamos calcular el límite:

\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}

Pero obtenemos la indeterminación ∞-∞.

De modo que primero debemos hacer la resta de las fracciones. Para ello, reducimos las fracciones a común denominador, esto es, multiplicamos el numerador y el denominador de una fracción por el denominador de la otra:

\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}

Y ahora que las dos fracciones tienen el mismo denominador, las podemos juntar en una sola fracción:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}

Operamos en el numerador y en el denominador:

\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}

Y finalmente volvemos a calcular el límite:

\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}

En este caso la indeterminación infinito entre infinito da +∞ porque el grado del numerador es mayor que el grado del denominador.

Indeterminación infinito menos infinito con raíces

Cuando la indeterminación infinito menos infinito se produce en una suma o resta de radicales, primero tenemos que multiplicar y dividir la función por la expresión radical conjugada y luego resolver el límite.

Vamos a ver cómo solucionar la indeterminación infinito menos infinito en una función irracional haciendo un ejemplo paso a paso:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)

Primero intentamos resolver el límite de la función con radicales:

\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}

Sin embargo, obtenemos la forma indeterminada ∞-∞. Así que para saber cuánto es la indeterminación infinito menos infinito debemos aplicar el procedimiento explicado.

Como la función tiene radicales, multiplicamos y dividimos toda la función por la expresión irracional conjugada:

\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}

La expresión algebraica del numerador corresponde a la identidad notable del producto de una suma por una diferencia, por lo tanto, podemos simplificar la expresión:

\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}

Ahora simplificamos la raíz del límite, ya que está elevada al cuadrado:

\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}

Operamos en el numerador de la fracción:

\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}

Y, por último, volvemos a hacer el cálculo del límite:

\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}

De manera que el resultado del límite es 0, porque cualquier número dividido entre infinito es igual a cero.

Ejercicios resueltos de límites al infinito

Ejercicio 1

Encuentra los siguientes límites de la función representada gráficamente:

\displaystyle\lim_{x\to -\infty}f(x)

\displaystyle\lim_{x\to +\infty}f(x)

\displaystyle\lim_{x\to -1^-}f(x)

\displaystyle\lim_{x\to -1^+}f(x)

\displaystyle\lim_{x\to 1^-}f(x)

\displaystyle\lim_{x\to 1^+}f(x)

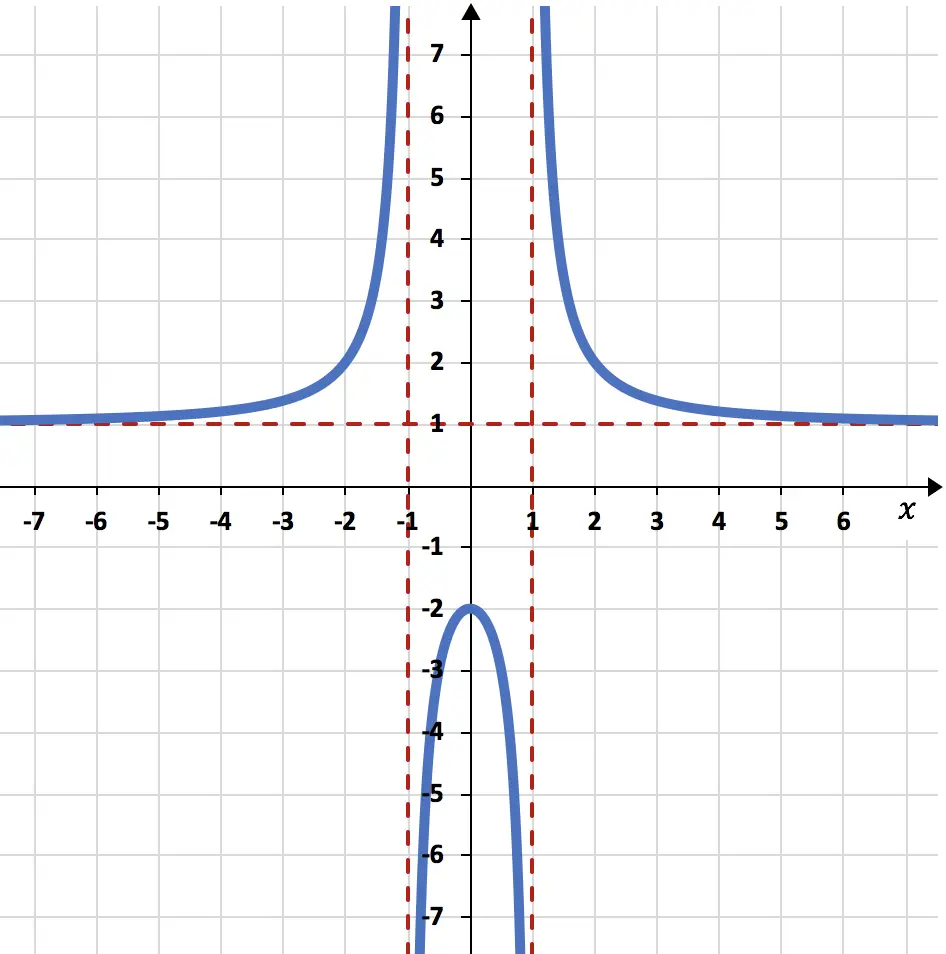
limites al infinito a partir de la representacion de una funcion

El límite de la función cuando x tiende a menos infinito y a más infinito dan 1:

\displaystyle\lim_{x\to -\infty}f(x)=1

\displaystyle\lim_{x\to +\infty}f(x)=1

Los límites laterales de la función por la izquierda y por la derecha en el punto x=-1 son más infinito y menos infinito respectivamente:

\displaystyle\lim_{x\to -1^-}f(x)=+\infty

\displaystyle\lim_{x\to -1^+}f(x)=-\infty

Finalmente, los límites laterales de la función cuando x tiende a 1 valen menos infinito y más infinito:

\displaystyle\lim_{x\to 1^-}f(x)=-\infty

\displaystyle\lim_{x\to 1^+}f(x)=+\infty

 

Ejercicio 2

Resuelve el límite cuando x tiende a más infinito de la siguiente función:

\displaystyle \lim_{x \to +\infty} (x^2+4x+1)

Para resolver el límite en el infinito tenemos que sustituir x por infinito en el término de mayor grado del polinomio:

\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}

 

Ejercicio 3

Calcula el límite en el infinito de la siguiente función polinómica:

\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)

Para resolver el límite al infinito sustituimos x por infinito en el término de mayor grado del polinomio y hacemos los cálculos:

\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}

 

Ejercicio 4

Resuelve el límite al menos infinito de la siguiente función polinómica:

\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)

Para calcular el límite al infinito sustituimos x por menos infinito en el término de mayor grado del polinomio y evaluamos la función:

\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}

Como el menos infinito está elevado al cuadrado, el signo del infinito cambia a positivo.

 

Ejercicio 5

Halla el límite en el infinito de la siguiente función racional:

\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}

Para determinar el límite al infinito sustituimos x por más infinito en el término de mayor grado del numerador y del denominador de la fracción:

\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}

Recuerda que cualquier número dividido entre más o menos infinito da como resultado 0.

 

Ejercicio 6

Resuelve el siguiente límite en el infinito:

\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)

Para calcular el límite cuando x tiende a ±∞ de una función solamente nos tenemos que fijar en el monomio de mayor grado de la función:

\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}

 

Ejercicio 7

Calcula el límite de la siguiente función cuando x tiende a menos infinito:

\displaystyle \lim_{x \to -\infty} (-4x^2+4)

En este caso simplemente debemos sustituir el infinito en el término cuadrático:

\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}

 

Ejercicio 8

Encuentra el límite de la siguiente función exponencial cuando x tiende a más infinito:

\displaystyle \lim_{x \to +\infty} 2^x

Aunque sea una función exponencial, el proceso para resolver el límite es el mismo: sustituir la x por el infinito.

\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}

 

Ejercicio 9

Resuelve el límite al infinito de la siguiente función exponencial:

\displaystyle \lim_{x \to +\infty} 5^{-x}

Para resolver este límite debemos usar las propiedades de las fracciones:

\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}

 

Ejercicio 10

Resuelve el siguiente límite al infinito:

\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}

El límite da la indeterminación menos infinito entre más infinito. El grado del numerador es mayor que el grado del denominador, por lo que el límite indeterminado es igual a más infinito. Sin embargo, como la división es infinito negativo entre infinito positivo, el resultado es menos infinito.

\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}

 

Ejercicio 11

Soluciona el siguiente límite indeterminado:

\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}

En este problema, la forma indeterminada infinito sobre infinito se consigue del cociente de dos polinomios con el mismo grado, por lo tanto, el resultado del límite indeterminado es la división de sus coeficientes principales:

\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}

 

Ejercicio 12

Calcula el siguiente límite al menos infinito:

\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}

El grado de la expresión algebraica del numerador es inferior al grado de la expresión del denominador, así que la indeterminación +∞/+∞ da 0:

\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}

 

Ejercicio 13

Resuelve el siguiente límite indeterminado de una función con raíces:

\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}

La expresión del numerador está bajo un radical, por lo que su grado es 7/3. Por otra parte, el polinomio del denominador es cuadrático. Y como 7/3>2, el límite da más infinito:

\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}

 

Ejercicio 14

Determina el límite al infinito de la siguiente función con fracciones:

\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}

En este ejercicio se obtiene la indeterminación menos infinito dividido por menos infinito con el grado del numerador mayor que el grado del denominador, por tanto:

\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}

 

Ejercicio 15

Halla el límite al menos infinito de la siguiente función:

\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}

El polinomio del denominador es cuadrático, mientras que el polinomio del numerador es lineal. Por lo tanto, la indeterminación infinito dividido por infinito da 0.

\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}

 

Ejercicio 16

Resuelve el límite al menos infinito de la siguiente función:

\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}

El numerador es de mayor grado que el denominador, así que el resultado de la forma indeterminada ∞/∞ será infinito. Además, el signo del infinito será negativo porque positivo entre negativo resulta en negativo:

\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}

 

Ejercicio 17

Soluciona el siguiente límite al infinito:

\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}

La función exponencial es de mayor orden que la función polinómica, por lo que el límite dará infinito. Sin embargo, al dividir positivo entre negativo, el signo del infinito será negativo:

\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}

 

Ejercicio 18

Calcula el límite al infinito de la siguiente función con una raíz cuadrada:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}

El numerador está compuesto por una raíz cuadrada, por lo que su grado es 2/2=1. Entonces, el grado del numerador es igual al del denominador, así que la indeterminación infinito entre infinito queda resuelta de la siguiente manera:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}

 

Ejercicio 19

Resuelve el límite al infinito de la siguiente función con dos radicales:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}

El grado del numerador es 7/3=2,33, y el grado del denominador es 5/2=2,5. Por lo tanto, como el grado del numerador es menor que el grado del denominador, el límite indeterminado infinito entre infinito es 0:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}

 

Ejercicio 20

Calcula el siguiente límite:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}

Independientemente del grado del numerador, como en el denominador tenemos una función exponencial, el resultado de la forma indeterminada infinito sobre infinito es 0:

\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}

 

Ejercicio 21

Determina el límite al infinito de la siguiente función racional:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)

En primer lugar, tratamos de hacer el cálculo del límite sustituyendo el infinito en la función:

\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}

Pero nos encontramos con la indeterminación ∞ – ∞. Por tanto, reducimos las fracciones a común denominador:

\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}

Y como ahora las dos fracciones tienen el mismo denominador, las podemos juntar en una sola fracción:

\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}

Efectuamos el paréntesis del numerador:

\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}

Y, finalmente, determinamos el límite:

\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}

En este caso la indeterminación ∞/∞ da +∞ porque el grado del numerador es mayor que el grado del denominador.

 

Ejercicio 22

Soluciona el límite de la siguiente función fraccionaria cuando x tiende a 0:

\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)

Primero intentamos calcular el límite como siempre:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}

Pero obtenemos la forma indeterminada ∞-∞. Por tanto, debemos reducir las fracciones de la función a común denominador.

En este caso, x4 es un múltiple de x2, así que solo multiplicando el numerador y el denominador de la segunda fracción por x2 ya conseguiremos que las dos fracciones tengan el mismo denominador:

\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}

Ahora ya podemos restar las dos fracciones:

\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}

Intentamos resolver el límite de nuevo:

\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}

Pero nos encontramos con la indeterminación de una constante partida por cero. Así que tenemos que calcular los límites laterales de la función.

\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty

En conclusión, como los dos límites laterales de la función en el punto x=0 dan como resultado -∞, la solución del límite es -∞:

\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}

 

Ejercicio 23

Resuelve el límite al infinito de la siguiente función con raíces:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)

Al intentar resolver el límite obtenemos la indeterminación infinito menos infinito:

\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}

Por tanto, como hay radicales en la función, debemos multiplicarla y dividirla por la expresión radical conjugada:

\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}

En el numerador tenemos el producto notable de una suma por una diferencia, que es igual a la diferencia de cuadrados. Por tanto:

\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}

Simplificamos el radical elevado al cuadrado:

\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}

Operamos en el numerador:

\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}

Y, para acabar, hallamos el límite:

\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}

En este caso la indeterminación infinito partido por infinito es más infinito porque el grado del numerador es más grande que el grado del denominador (recuerda que la raíz cuadrada reduce el grado entre dos: \sqrt{x^4} = x^{4/2} = x^2 ).

 

Ejercicio 24

Resuelve el límite cuando x tiende al infinito de la siguiente función irracional:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)

Primero de todo, tratamos de calcular el límite como siempre:

\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}

Pero nos da como resultado la indeterminación de la diferencia de infinitos. Por tanto, como la función tiene raíces, debemos multiplicar y dividir la expresión por el conjugado radical:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}

Agrupamos la igualdad notable del numerador de la fracción:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}

Resolvemos la raíz cuadrada:

\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Resolvemos la identidad notable del cuadrado de una diferencia:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}

Operamos en el numerador:

\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}

\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}

Y, por último, calculamos el valor del límite al infinito:

\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =

Aunque haya una x al cuadrado en el denominador, su grado en verdad es 1 porque está dentro de una raíz: \sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .

Por tanto, el resultado de la indeterminación -∞/+∞ es la división de los coeficientes de las x de mayor grado, ya que el grado del numerador es igual que el grado del denominador.

\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}

Fíjate que como hay dos términos de primer grado en el denominador \bigl(2x y \sqrt{4x^2}\bigr), para resolver la indeterminación -∞/+∞ tenemos que coger todos los coeficientes de los términos de primer grado, es decir, el 2 de 2x y el \sqrt{4} de \sqrt{4x^2}.

 

Ejercicio 25

Calcula el límite cuando x tiende a 1 de la siguiente función con fracciones:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)

Al intentar hacer el límite obtenemos el límite indeterminado de infinito menos infinito:

\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}

De manera que debemos reducir las fracciones a común denominador, o dicho con otras palabras, tenemos que multiplicar el numerador y el denominador de una fracción por el denominador de la otra:

\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}

Y como ahora las dos fracciones tienen el mismo denominador, las podemos juntar:

\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}

Operamos:

\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}

\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}

Y volvemos a intentar resolver el límite:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}

Pero nos encontramos con la indeterminación cero partido por cero. Así que tenemos que factorizar los polinomios del numerador y del denominador:

\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}

Ahora simplificamos la fracción quitando el factor que se repite en el numerador y en el denominador:

\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}

Y, finalmente, resolvemos el límite:

\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}

 

8 comentarios en “Límites al infinito”

  1. Juan David

    Hola, ¿El autor tiene más páginas de este tipo?, si es así, ¿podría compartirme los enlaces porfavor? encontré la de Matrices y determinantes pero estoy interesado también en otros temas como vectores, rectas y planos en el espacio etc. La forma en la que explica y deja ejercicios me gusta mucho.

    Responder
    1. Funciones

      Hola Juan David,

      Efectivamente, y de hecho hay una página web dedicada exclusivamente a los temas que mencionas. Te dejo las páginas webs hermanas a continuación:

      matricesydeterminantes.com
      geometriaanalitica.info
      polinomios.org
      ejerciciosecuaciones.com
      areasyvolumenes.net
      probabilidadyestadistica.net

      ¡Aunque algunas aún están en construcción! 😉

  3. Marcela

    Muy bien explicado, y los ejercicios muy representativos! Felicitaciones!! Tendras material de derivadas e integrales de una sola variable? Muchas gracias!!

    Responder
    1. Funciones

      Hola Marcela,

      ¡Muchas gracias por tu comentario!

      Tienes la teoría de derivadas de una variable junto con ejercicio resueltos en esta misma página web (puedes acceder desde la página de inicio), por otro lado, está previsto añadir temario sobre integrales en un futuro. 🙂

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *