Cómo interpolar una función: Interpolación Lineal y Cuadrática

En esta página encontrarás qué significa interpolar una función. En concreto, se explica la interpolación lineal y la interpolación cuadrática. Además, podrás ver varios ejemplos para que no te quede ninguna duda de cómo se interpola una función.

Índice

¿Qué es la interpolación de una función?

La definición de interpolación es la siguiente:

En matemáticas, la interpolación es un procedimiento que se utiliza para aproximar el valor que toma una función en un punto situado en un intervalo del cual se conocen los puntos extremos.

¿Cuál es la diferencia entre la interpolación y la extrapolación?

Interpolar y extrapolar tienen significados muy parecidos, ya que ambos implican estimar el valor de una función en un punto a partir de dos puntos conocidos.

Sin embargo, interpolar implica hacer una aproximación de un punto situado dentro del intervalo que forman estos dos puntos conocidos. En cambio, extrapolar significa estimar el valor de la función en un punto ubicado fuera del intervalo que componen estos dos puntos conocidos.

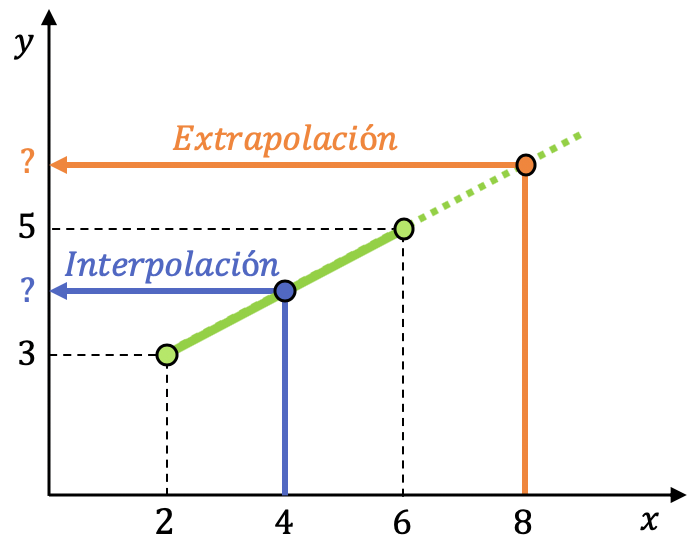
interpolacion y extrapolacion o interpolar y extrapolar

Como puedes ver en la gráfica anterior, los puntos conocidos son (2,3) y (6,5). En este caso queremos interpolar en x=4, ya que está entre los puntos conocidos, y, por contra, queremos extrapolar en x=8, porque está fuera del intervalo conocido.

Evidentemente, un valor interpolado es mucho más fiable que un valor extrapolado, debido a que en la extrapolación estamos suponiendo que la función seguirá un trazado similar. Sin embargo, podría ser que la pendiente de la función cambiara fuera de los límites del intervalo conocido y entonces la estimación sería errónea.

Interpolación lineal

La interpolación lineal es un caso particular de la interpolación polinómica de Newton. En este caso se usa un polinomio de primer grado, es decir una función lineal o afín, para adivinar el valor de la función en un punto.

Dados dos puntos conocidos, $P_1(x_1,y_1)$ y $P_2(x_2,y_2)$ , la fórmula para realizar la interpolación lineal es:

$y=\cfrac{y_2-y_1}{x_2-x_1}\cdot(x-x_1) + y_1$

Donde $x$ e $y$ son las coordenadas del punto interpolado.

Se puede comprobar que esta fórmula corresponde a la ecuación punto-pendiente de la recta.

Ejemplo de cómo interpolar linealmente

A continuación vamos a ver un problema a modo de ejemplo para acabar de entender el concepto de interpolación lineal:

En una fábrica se producen en 4 horas 2 artículos, y en 8 horas 10 artículos. Si el número de artículos producidos tienen una relación lineal con las horas trabajadas, ¿cuántos artículos se fabricarán en 5 horas?

Primero de todo tenemos que definir la función lineal que relaciona las horas trabajadas con los artículos producidos. En este caso las X serán las horas trabajadas y las Y serán los artículos que se fabrican. Porque se fabricarán más o menos artículos en función de las horas trabajadas, o dicho de otra forma, la producción depende de las horas, y no al revés.

A partir del enunciado sabemos que la función pasa por los puntos (4,2) y (8,10). Por lo tanto, simplemente tenemos que aplicar la fórmula para interpolar en el punto $x=5:$

$y=\cfrac{y_2-y_1}{x_2-x_1}\cdot(x-x_1) + y_1$

Sustituimos los valores de los puntos en la ecuación:

$y=\cfrac{10-2}{8-4}\cdot(5-4) + 2$

Y hacemos las operaciones:

$y=\cfrac{8}{4}\cdot1 + 2 = 2\cdot 1 +2 = 4$

$\bm{y=4}$

De modo que con 5 horas se producirán 4 artículos.

Interpolación cuadrática

La interpolación cuadrática consiste en hacer la interpolación con un polinomio de segundo grado en vez de un polinomio de grado 1. Por tanto, en este caso se utiliza una función cuadrática o parábola.

$y = ax^2+bx+c$

En general, la interpolación de segundo orden es más precisa que la de primer orden, ya que es de mayor grado. Por contra, se necesita un punto más para poder llevar a cabo la interpolación.

El matemático Lagrange desarrolló una fórmula para hallar la función interpoladora de orden n-ésimo. Para el caso de orden 2, el polinomio interpolador de Lagrange es el siguiente:

$y=\cfrac{(x-x_1)(x-x_2)}{(x_0-x_1)(x-x_2)}\cdot y_0+ \cfrac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_0-x_2)}\cdot y_1+ \cfrac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}\cdot y_2$

Donde los puntos conocidos $P_1(x_1,y_1)$ , $P_2(x_2,y_2)$ y $P_3(x_3,y_3)$ sirven para encontrar el valor de la función en la abscisa $x.$

Sin embargo, en la práctica no se suele utilizar el método de interpolación de Lagrange, sino que se calcula la función cuadrática a partir de los 3 puntos observados y luego se evalúa el punto a interpolar en la función. A continuación dispones de un ejercicio resuelto para ver cómo se hace:

Ejemplo de cómo interpolar cuadráticamente

Determina la función cuadrática que pasa por los puntos (0,1), (1,0) y (3,4) y luego interpola el valor de $x=-1.$

Como las funciones cuadráticas son polinomios de segundo orden, la función interpoladora será de la siguiente forma:

$y = ax^2+bx+c$

De modo que debemos calcular los coeficientes $a$ , $b$ y $c$ . Para ello, sustituimos las coordenadas de los puntos conocidos en la función:

$\left.\begin{array}{l} 1 = a\cdot 0^2+b\cdot 0+c \\[2ex] 0 = a\cdot 1^2+b\cdot 1+c \\[2ex] 4 = a\cdot 3^2+b\cdot 3+c \end{array} \right\} \longrightarrow \left.\begin{array}{l} 1 = c \\[2ex] 0 = a+b+c \\[2ex] 4 = 9a+3b+c \end{array} \right\}$

Ahora resolvemos el sistema de ecuaciones:

$\left.\begin{array}{l} 1 = c \\[2ex] 0 = a+b+c \\[2ex] 4 = 9a+3b+c \end{array} \right\} \begin{array}{l} \\[2ex] \xrightarrow{c \ = \ 1} \\[2ex] & \end{array} \left.\begin{array}{l} c=1 \\[2ex] 0 = a+b+1 \\[2ex] 4 = 9a+3b+1 \end{array}\right\}$

Ya conocemos el valor de $c$ , así que podemos resolver el sistema con el método de sustitución: despejamos la incógnita $a$ de la segunda ecuación y sustituimos la expresión encontrada en la última ecuación:

$\left.\begin{array}{l} a=-b-1 \\[2ex] 4 = 9a+3b+1 \end{array}\right\}\longrightarrow \left.\begin{array}{l} a=-b-1 \\[2ex] 4 = 9(-b-1)+3b+1 \end{array}\right\}$

Hallamos la incógnita $b$ a partir de la última ecuación:

$4 = -9b-9+3b+1$

$12 =-6b$

$b=\cfrac{12}{-6} = -2$

Y encontramos el valor de $a$ con la segunda ecuación del sistema:

$a=-(-2)-1 = 1$

De manera que la función cuadrática es la siguiente:

$\bm{y = x^2-2x+1}$

Por último, interpolamos la abscisa $x=-1$ para calcular el valor de la función en este punto:

$y=(-1)^2-2\cdot(-1)+1=1+2+1=\bm{4}$

Aplicaciones de la interpolación

Aunque quizá no lo parece, la interpolación es muy útil en las matemáticas y la estadística. Por ejemplo, sirve para intentar predecir el valor de una función: a partir de una serie de datos recogidos se calcula la recta de regresión y con ella se puede tener una aproximación de cuánto valdrá la función en cada punto.

La interpolación de una función se puede realizar manualmente, como hemos visto, o con programas informáticos como Excel o MATLAB. Obviamente, es mucho más cómodo y rápido hacerlo mediante un ordenador.

Por otro lado, la interpolación también se utiliza para simplificar cálculos. Hay determinados softwares que deben realizar cálculos complejos con funciones muy largas, por lo que, a veces, se realiza una interpolación lineal de dichas funciones para simplificar las operaciones.

Interpolación lineal y cuadrática