En esta página se explica el significado de extrapolar una función. También encontrarás un ejemplo de cómo realizar una extrapolación lineal y, finalmente, las diferencias que hay entre la interpolación y la extrapolación.
Índice
¿Qué es la extrapolación?
La definición de extrapolación es la siguiente:
En matemáticas, la extrapolación es un proceso que se utiliza para aproximar el valor que toma una función en un punto situado fuera de un intervalo observado.
Por lo tanto, al extrapolar siempre estamos suponiendo que la función será de una determinada manera ya que no tenemos datos más allá de los límites del intervalo. En consecuencia, nunca se puede garantizar completamente que la función tomará ese valor aproximado.
¿Cuál es la diferencia entre la interpolación y la extrapolación?
Interpolar y extrapolar tienen significados muy parecidos, ya que ambos implican estimar el valor de una función en un punto a partir de dos puntos conocidos.
Sin embargo, extrapolar significa estimar el valor de la función en un punto ubicado fuera del intervalo que componen estos dos puntos conocidos. En cambio, interpolar implica hacer una aproximación de un punto situado dentro del intervalo que forman estos dos puntos conocidos.
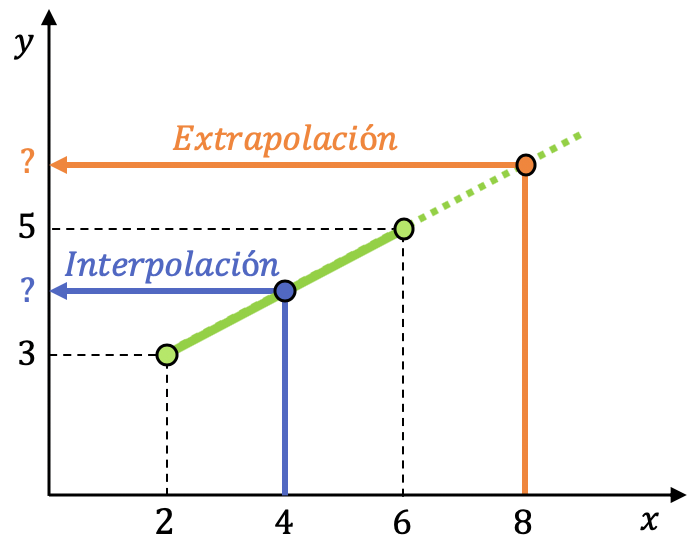
Como puedes ver en la gráfica anterior, los puntos conocidos son (2,3) y (6,5). En este caso queremos hacer una interpolación en x=4, ya que está entre los puntos conocidos, por contra, pretendemos realizar una extrapolación en x=8, porque está fuera del intervalo conocido.
Evidentemente, un valor interpolado es mucho más fiable que un valor extrapolado, debido a que en la extrapolación estamos suponiendo que la función seguirá un trazado similar. Sin embargo, podría ser que la pendiente de la función cambiara fuera de los límites del intervalo conocido y entonces la estimación sería errónea. Por esa razón la predicción del valor es más fiable cuanto más cerca está el punto extrapolado del intervalo conocido.
Extrapolación lineal
Extrapolar de manera lineal quiere decir aproximar la función a una función lineal o afín, es decir, a una función polinómica de grado 1.
La manera más fácil de llevar a cabo una extrapolación lineal es mediante la interpolación polinómica de Newton. En este caso se usa un polinomio de primer grado para intentar predecir el valor de la función en un punto.
Dados dos puntos conocidos, y
, la fórmula para realizar la extrapolación lineal es:
Donde e
son las coordenadas del punto extrapolado.
Se puede comprobar que esta fórmula corresponde a la ecuación punto-pendiente de la recta.
Ejemplo de cómo extrapolar linealmente
A continuación vamos a ver un problema a modo de ejemplo para acabar de entender el concepto de extrapolación lineal:
- El precio por persona de un viaje en autocar depende linealmente de los quilómetros recorridos. Recorrer 70 km cuesta 15€ y 120 km cuesta 20€. Calcula el precio de un trayecto de 150 km.
Primero de todo tenemos que definir la función lineal que relacione los quilómetros recorridos con el precio del trayecto. En este caso las X serán los quilómetros recorridos y las Y será el precio. Porque el precio variará en función de los quilómetros realizados, o dicho de otra forma, el precio depende de los quilómetros hechos, y no al revés.
A partir del enunciado sabemos que la función pasa por los puntos (70,15) y (120,20). Por lo tanto, simplemente tenemos que aplicar la fórmula para extrapolar en el punto
Sustituimos los valores de los puntos en la ecuación:
Y hacemos los cálculos:
De modo que hacer un trayecto de 150 km costará 23€.
De esta forma ya hemos resuelto el ejercicio, como has visto no es muy complicado. ¡Recuerda que puedes dejar cualquier duda que tengas en los comentarios!
