Hallar la ecuación de la recta tangente (ejercicios resueltos)

En este post veremos cómo encontrar la ecuación de la recta tangente a una curva. Además, podrás practicar con ejercicios resueltos de diferentes niveles de dificultad.

Índice

Ecuación de la recta tangente a una función en un punto

La ecuación de la recta tangente a la función f(x) en el punto x=x₀ es:

$y -y_0= m(x-x_0)$

Donde el punto P(x₀,y₀) es el punto donde coinciden la recta tangente y la función. Y la pendiente de la recta tangente, m, es igual a la derivada de la curva en el punto x₀, es decir, m=f'(x₀).

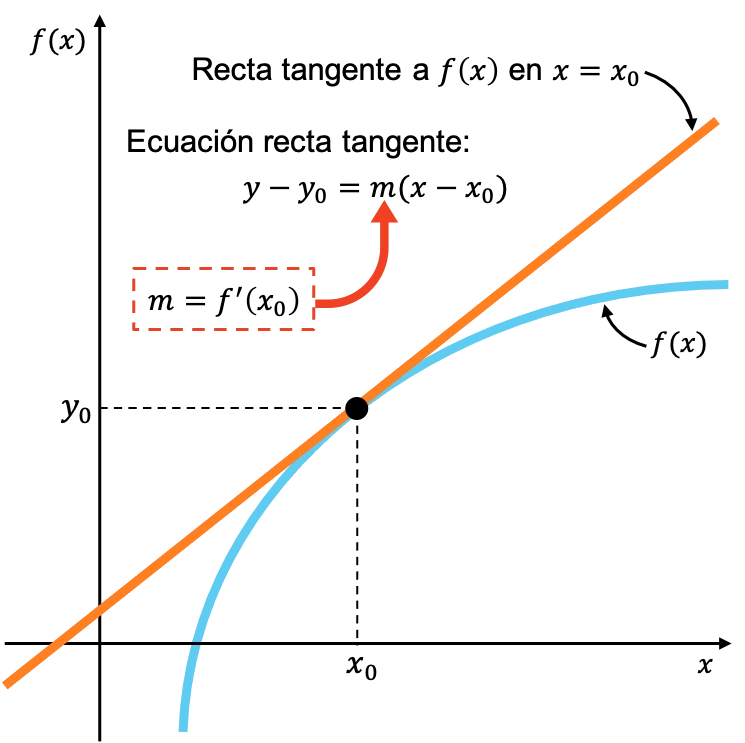
En la imagen de arriba puedes ver una curva $f(x)$ representada de color azul, y una recta de color naranja que es tangente a la función $f(x)$ en el punto $x=x_0$ , ya que únicamente tienen ese punto en común. Pues la ecuación de esta recta tangente es $y -y_0= m(x-x_0)$ , y su pendiente es $m=f'(x_0)$ .

Cómo hallar la ecuación de la recta tangente

Para hallar la ecuación de la recta tangente a una función en un punto, se debe hacer:

Hallar la pendiente de la recta tangente calculando la derivada de la función en el punto de tangencia.
Determinar un punto de la recta tangente.
Hallar la ecuación de la recta tangente utilizando la pendiente y el punto de la recta tangente calculados.

Ejemplo de la ecuación de la recta tangente a una curva

Una vez hemos visto la teoría sobre la ecuación de la recta tangente, vamos a ver cómo se calcula la ecuación de una recta tangente resolviendo un ejemplo paso a paso:

Calcula la ecuación de la recta tangente a la curva $f(x)=x^2+x$ en el punto $x=1$ .

Sabemos que la ecuación de la recta tangente siempre es de la siguiente forma:

$y -y_0= m(x-x_0)$

Lo primero que debemos hacer es calcular la pendiente de la recta. Así pues, la pendiente de la recta tangente, $m$ , será el valor de la derivada de la curva en el punto de tangencia x=1, es decir $m=f'(1).$ Así que derivamos la función y luego calculamos $f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Una vez conocemos el valor de $m$ , tenemos que hallar un punto $(x_0,y_0)$ de la recta tangente para completar la ecuación de la recta tangente.

La ecuación de la recta tangente y la curva siempre tienen un punto en común, que en este caso es $x=1$ . Por tanto, como la curva $f(x)$ pasa por este punto, podemos hallar la otra componente del punto calculando $f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Así que el punto de tangencia es:

$P(1,2)$

Por este punto pasan tanto la curva como la recta tangente, de modo que también lo podemos utilizar para hallar la ecuación de la recta tangente.

Ahora simplemente tenemos que sustituir los valores encontrados de la pendiente y el punto de la recta tangente en su ecuación:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

En definitiva, la ecuación de la recta tangente es:

$\bm{y-2=3(x-1)}$

También se puede expresar la ecuación de la recta tangente con la ecuación explícita de la recta:

$\bm{y=3x-1}$

A continuación puedes ver representadas la curva $f(x)=x^2+x$ y su recta tangente en $x=1,$ $y-2=3(x-1):$

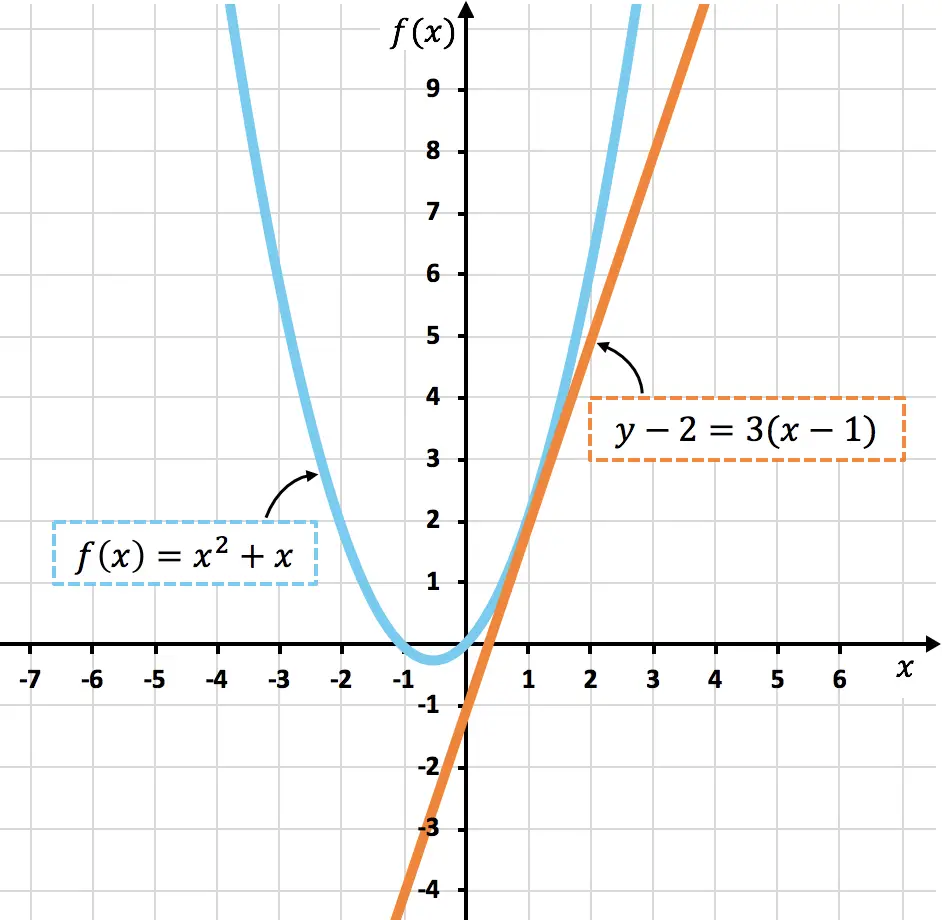
ecuacion de la recta tangente a una curva en un punto

Como puedes ver, la curva $f(x)=x^2+x$ y la recta tangente $y-2=3(x-1)$ solamente tienen en común el punto $(1,2)$ , tal y como habíamos calculado.

Ejercicios resueltos de la ecuación de la recta tangente

Ejercicio 1

Calcula la ecuación de la recta tangente a la curva $f(x)=2x^2-4x+3$ en el punto $x=2 .$

Ver solución

La ecuación de la recta tangente siempre será de la siguiente forma:

$y-y_0=m(x-x_0)$

Paso 1: Calcular la pendiente de la recta tangente

La pendiente, m, es el valor de la derivada de la curva en el punto de tangencia. Por tanto, en este caso $m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Paso 2: Hallar un punto de la recta tangente

La ecuación de la recta tangente y la curva siempre tienen un punto en común, que en este caso es $x=2$ . Por tanto, como la curva $f(x)$ pasa por este punto, podemos hallar la otra componente del punto calculando $f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Así que el punto por el que pasan tanto la curva como la recta tangente es el punto $(2,3).$

Paso 3: Escribir la ecuación de la recta tangente

Ahora simplemente tenemos que sustituir los valores encontrados de la pendiente y el punto de la recta tangente en su ecuación:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

Así que la ecuación de la recta tangente es:

$\bm{y -3= 4(x-2)}$

Ejercicio 2

Calcula la ecuación de la recta tangente a la curva $\displaystyle f(x)=-3x^2+2x$ en el origen de coordenadas.

Ver solución

El origen de coordenadas se refiere al punto $(0,0).$ De modo que tenemos que calcular la recta tangente a la función en el punto $(0,0) .$

En primer lugar, determinamos el valor de la pendiente de la recta tangente calculando la derivada en el origen de coordenadas:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

En este caso ya conocemos un punto por el que pase la recta tangente. Porque el enunciado nos dice que la recta debe ser tangente a la curva en el origen de coordenadas, es decir en el punto $(0,0).$

Así que el punto que comparten la curva y la recta tangente es el punto $(0,0).$

Finalmente, solo nos queda sustituir los valores hallados de la pendiente y el punto de la recta tangente en su ecuación:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

En conclusión, la ecuación de la recta tangente es:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Ejercicio 3

Calcula la recta tangente a la curva $f(x)=x^2-2x-1$ que es paralela a la recta $y-4x-6=0$ .

Ver solución

En este problema nos dicen que la recta tangente tiene que ser paralela a la recta $y-4x-6=0 .$ Y dos rectas son paralelas si tienen la misma pendiente. Por tanto, la recta tangente debe tener la misma pendiente que la recta $y-4x-6=0.$

Esto significa que debemos hallar la pendiente de la recta $y-4x-6=0 .$ Para ello, despejamos la variable y:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

De manera que la pendiente de la recta $y=4x+5$ es 4, ya que la pendiente de una recta es el número que multiplica a la x cuando la y está despejada.

En consecuencia, la pendiente de la recta tangente también tiene que ser 4, ya que para que sean paralelas deben tener la misma pendiente.

$m=4$

En este caso no nos dicen el punto de tangencia entre la curva y la recta tangente. Pero sabemos que la derivada de la curva en el punto de tangencia es igual a la pendiente de la recta tangente, es decir $m=f'(x_0)$ . Pues como sabemos el valor de $m$ , podemos hallar x₀ de la ecuación $m=f'(x_0):$

Para ello primero calculamos la derivada de $f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

Y ahora resolvemos $m=f'(x_0)$ sabiendo que $m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

Y una vez sabemos la coordenada x del punto, podemos hallar la otra coordenada del punto calculando $f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Así que el punto por el que pasan tanto la curva como la recta tangente es el punto $(3,2).$

Ahora simplemente tenemos que sustituir los valores encontrados de la pendiente y el punto de la recta tangente en su ecuación:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

Y la ecuación de la recta tangente es:

$\bm{y -2=4(x-3)}$

Ejercicio 4

Calcula la recta tangente a la curva $f(x)=2x^2+5x+1$ que forma un ángulo de 45º con el eje X.

Ver solución

El enunciado del problema nos dice que la recta tangente debe formar un ángulo de 45º con el eje X. En estos casos se tiene que aplicar la siguiente fórmula para hallar el valor de la pendiente:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

El enunciado no dice el punto de tangencia entre la curva y la recta tangente. Pero sabemos que la derivada de la curva en el punto de tangencia es equivalente a la pendiente de la recta tangente, es decir $m=f'(x_0)$ . Entonces, podemos calcular x₀ resolviendo la ecuación $m=f'(x_0):$

Para ello primero calculamos la derivada de $f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$

Y ahora resolvemos $m=f'(x_0)$ sabiendo que $m = 1 :$

$m =f'(x_0)$

$1 =4(x_0)+5$

$1-5 =4x_0$

$-4 =4x_0$

$\cfrac{-4}{4} =x_0$

$-1=x_0$

Y una vez sabemos la coordenada x del punto, podemos hallar la otra coordenada del punto calculando $f(-1):$

$f(-1)=2(-1)^2+5(-1)+1=2\cdot 1 -5 + 1 = -2$

Así que el punto por el que pasan tanto la curva como la recta tangente es el punto $(-1,-2).$

Ahora simplemente tenemos que sustituir los valores encontrados de la pendiente y el punto de la recta tangente en su ecuación:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=1 \qquad P(-1,-2) \end{array} \right\} \longrightarrow \ y -(-2)= 1(x-(-1))$

Y, por último, hacemos las operaciones para encontrar la ecuación de la recta tangente es:

$y -(-2)=1(x-(-1))$

$y +2=1(x+1)$

$\bm{y + 2=x+1}$

6 comentarios en “Ecuación de la recta tangente”

Emilia
08/02/2022 a las 20:25

la ecuación de la recta tangente a la curva con ecuación 𝑓(𝑥) = x2 − 3𝑥, en el punto
(1,-2)

Responder
1. Funciones
  16/02/2022 a las 00:20
  
  Buenas Emilia,
  
  En primer lugar, calculamos la derivada de la curva:
  
  $f'(x)=2x-3$
  
  Luego hallamos el valor de la derivada en la coordenada X del punto:
  
  $f'(1)=2\cdot 1-3=-1$
  
  Por tanto, la pendiente de la recta tangente es -1 y sabemos un punto de la recta (1,-2), con estos datos podemos determinar ecuación de la recta tangente:
  
  $y-(-2)=-1(x-1)$
  
  $y+2=-x+1$
Pablo Hidalgo
21/02/2022 a las 16:24

Sea f(x)=2x−12−x . Obtenga la recta tangente en (1, 1)

Responder
1. Funciones
  23/02/2022 a las 00:40
  
  Hola Pablo,
  
  En primer lugar, calculamos la derivada de la función en el punto x=1:
  
  $f'(x)=2-0-1=1$
  
  $f'(1)=1$
  
  De manera que la ecuación punto-pendiente de la recta tangente es:
  
  $y-1=1(x-1)$
Gisela
05/03/2022 a las 07:45

La pendiente de una recta tangente a una curva es: x + 3. Obtén la ecuación de la curva si pasa por el punto (2, 4) Toma en cuenta que la integral es la inversa de la derivada y que, al derivar la ecuación de una curva, podemos encontrar la pendiente en ese punto.

Responder
1. Funciones
  09/03/2022 a las 15:13
  
  Hola Gisela,
  
  Mediante un proceso de integración podemos calcular la expresión de la curva:
  
  $\displaystyle f(x)=\int (x+3)dx= \cfrac{x^2}{2}+3x+k$
  
  Además, como sabemos que la curva pasa por el punto (2,4), podemos hallar el valor de la constante de integración sustituyendo las coordenadas del punto en la ecuación:
  
  $f(2)=4$
  
  $\cfrac{2^2}{2}+3\cdot 2+k=4$
  
  $k=-4$
  
  En conclusión, la ecuación de la curva es:
  
  $f(x)=\cfrac{x^2}{2}+3x-4$

Ecuación de la recta tangente a una función en un punto

Cómo hallar la ecuación de la recta tangente

Ejemplo de la ecuación de la recta tangente a una curva

Ejercicios resueltos de la ecuación de la recta tangente

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

6 comentarios en “Ecuación de la recta tangente”

Deja un comentario Cancelar respuesta