En este post explicamos qué son el dominio y el recorrido (o imagen) de una función y cómo calcularlos, tanto gráficamente como numéricamente. Además, verás un ejemplo de cómo se hace y encontrarás varios ejercicios resueltos paso a paso de para que puedas practicar.
Índice
¿Qué es el dominio y el recorrido de una función?
Las definiciones de dominio y recorrido de una función son las siguientes:
El dominio de una función real son todos los valores de x en los que existe la función. El dominio de una función se representa con la expresión Dom f.
El recorrido de una función, o imagen de una función, son todos los valores de f(x) donde existe la función. El recorrido de una función se representa con la expresión: Im f.
En matemáticas el dominio de una función también se puede decir dominio de definición o campo de existencia. Y, por otro lado, hay matemáticos que también llaman al recorrido de una función como rango de una función.
Dominio y recorrido de una función a partir de una gráfica
Entenderemos mejor el concepto de dominio y recorrido con un ejemplo. Vamos a analizar el dominio y el recorrido de la siguiente función:
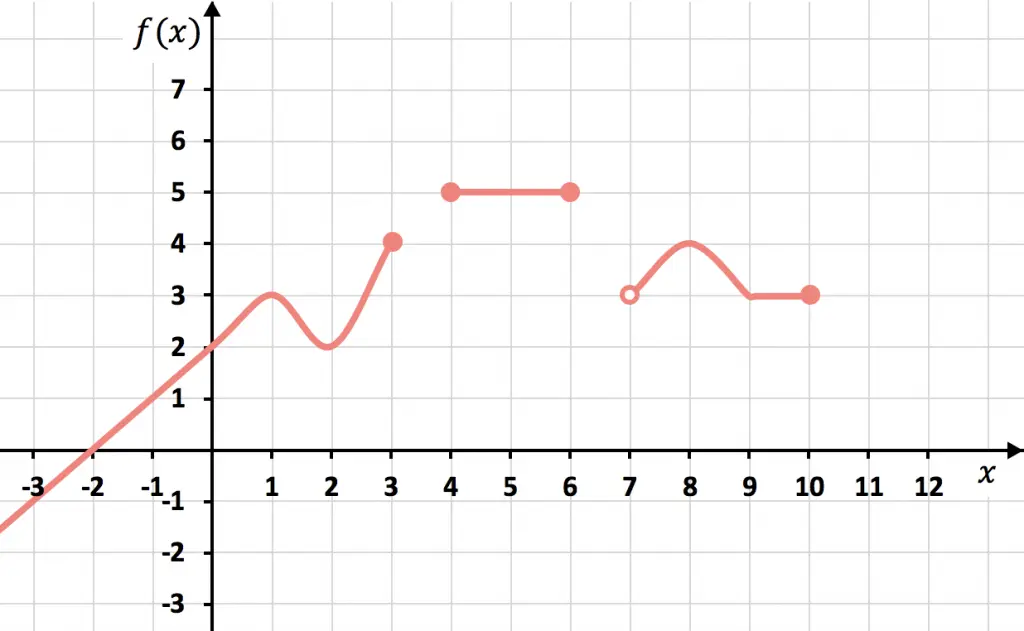
Primero examinaremos el dominio de la función, por lo que nos tenemos que fijar en el eje horizontal. La función viene desde (porque no vemos donde empieza y no tiene ningún punto fijo al prinicipio) y existe hasta
. Además, entre
y
también existe la función. Y la función existe incluso desde
(no incluido) hasta
, donde se acaba. Así que el dominio de la función es:
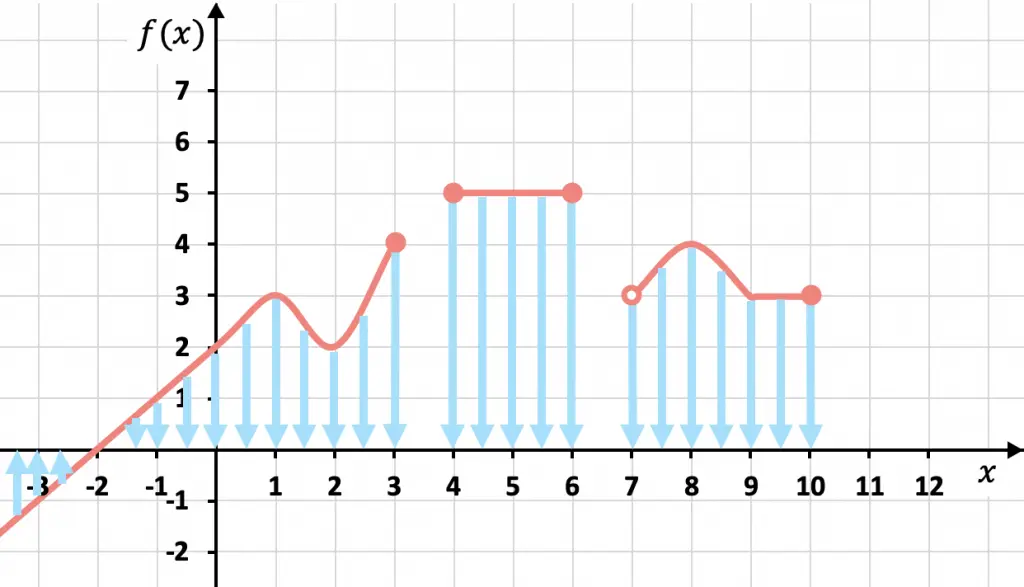
Si te fijas, desde hasta
no existe la función, por lo tanto, este tramo no pertenece al domino de la función. Y lo mismo sucede con el tramo entre
y
, donde la función tampoco existe. Por eso no hemos incluido estos tramos en el dominio.
Recuerda que si tenemos un punto abierto, como en , hay que poner un paréntesis
o
, que indica que ese punto no está incluido, es decir que la función no existe en ese punto. En cambio, si tenemos un punto cerrado, como en
, hay que poner un corchete
o
, que indica que ese punto sí que está incluido. Asimismo, el infinito siempre va acompañado de un paréntesis ya sea positivo o negativo.
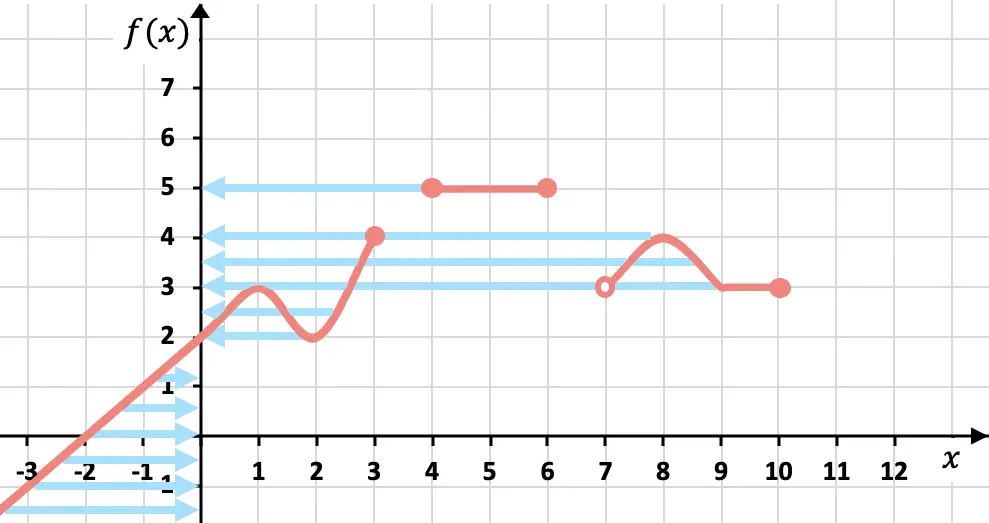
Ahora vamos analizar el recorrido de la función, y para ello nos tenemos que fijar en el eje vertical. La función viene desde y existe hasta
, por lo tanto, este tramo pertenece al recorrido de la función. Además, la función también existe cuando
. Pero en cualquier otro valor de
la función no existe, así que el recorrido o imagen de esta función es:
Calcular el dominio de una función numéricamente
Hay algunas funciones típicas en las que se puede calcular el dominio numéricamente. Vamos a ver cada caso uno por uno:
Dominio de una función polinómica
Las funciones polinómicas son aquellas funciones que consisten en un polinomio simple. Es decir que no tienen ni raíces ni denominadores, sino que simplemente aparecen elevadas a un coeficiente sumando o restando. Por ejemplo:
En este tipo de funciones no existe ningún valor de que haga que no exista la función. Por tanto,
existe siempre, o dicho de otra forma, el dominio son todos los números reales:
Por ejemplo, vamos a encontrar el dominio de la siguiente función polinómica:
Como se trata de una función polinómica, su dominio son todos los números reales:
Dominio de una función racional
Las funciones racionales son aquellas en las que la incógnita aparece en el denominador de una fracción. Por ejemplo:
Un número dividido entre 0 es una indeterminación que da como resultado infinito (∞). Por tanto, una función racional existirá siempre menos cuando el denominador sea 0.
De modo que para sacar el dominio de una función racional debemos encontrar cuándo es 0 el denominador, ya que ese punto será el único que no pertenece al dominio.
Veamos cómo se hace con un ejemplo. Calcularemos el dominio de la siguiente función con fracciones:
Al ser una función racional, tenemos que igualar a 0 el denominador y resolver la ecuación:
Por tanto, cuando x sea -2 el denominador será 0. Y, en consecuencia, la función no existirá. Así que el domino de la función son todos los números excepto x=-2. Esto se indica de la siguiente manera:
Dominio de una función radical de índice par
Las funciones radicales son aquellas funciones en las que la incógnita aparece en una raíz. En este caso nos centraremos en las funciones con raíces con índice par, como por ejemplo:
No existe la raíz (de índice par) de un número negativo. Por tanto, la función radical con índice par existirá siempre que su contenido sea igual o más grande que 0.
Veamos cómo se calcula con un ejemplo. Calcularemos el dominio de la siguiente función formada por una raíz:
Consiste en una función radical con índice par, por tanto miramos cuándo su contenido es positivo o nulo:
Resolvemos la inecuación:
De manera que la función existirá siempre que x sea mayor o igual que 4, que se indica con este intervalo:
Dominio de una función radical de índice impar
Las funciones radicales de índice impar no tienen este problema, ya que sí que existe la raíz de índice impar de un número negativo:
En consecuencia, las funciones radicales de índice impar existen por cualquier valor de . O, dicho con otras palabras, el dominio son todos los números reales:
Por ejemplo, vamos a calcular el dominio de la siguiente función radical cuyo índice es impar:
Como se trata de una función radical con índice impar, su dominio son todos los números reales:
Dominio de una función exponencial
Las funciones exponenciales son aquellas en que la forma parte del exponente de un número, como por ejemplo:
Las funciones exponenciales existen por cualquier valor de . Por tanto, el dominio son todos los números reales:
Por ejemplo, vamos a ver cómo se calcula el dominio de la siguiente función exponencial:
Como se trata de una función exponencial, su dominio son todos los números reales:
Dominio de una función logarítmica
Las funciones logarítmicas son aquellas que estan formadas por logaritmos, como por ejemplo:
El argumento de un logaritmo siempre debe ser positivo, por lo tanto, el dominio de una función logarítmica son todas las que hacen positivo el argumento.
Veamos cómo se determina el dominio mediante un ejemplo. Calcularemos el dominio de la siguiente función logarítmica:
Es una función logarítmica, por lo que miramos cuándo su argumento es positivo (mayor que 0):
Resolvemos la inecuación:
Así que la función existirá siempre que sea más grande 3, que se indica con este intervalo:
Dominio de las funciones trigonométricas
En este artíuclo solamente estudiaremos el dominio de las funciones trigonométricas básicas: el seno, el coseno y la tangente. Pero puedes consultar cómo se encuentra el dominio de funciones trigonométricas más complejas en la web.
Las funciones seno y coseno siempre existen independientemente del valor que tome , de modo que sus dominios son todos los números reales:
Sin embargo, la función tangente no existe en los múltiplos impares de por lo que su dominio son todos los números reales excepto esos números:
Ejercicios resueltos de dominio y recorrido de una función
Ejercicio 1
Determina el dominio y el recorrido de la siguiente función definida a trozos a partir de la gráfica:
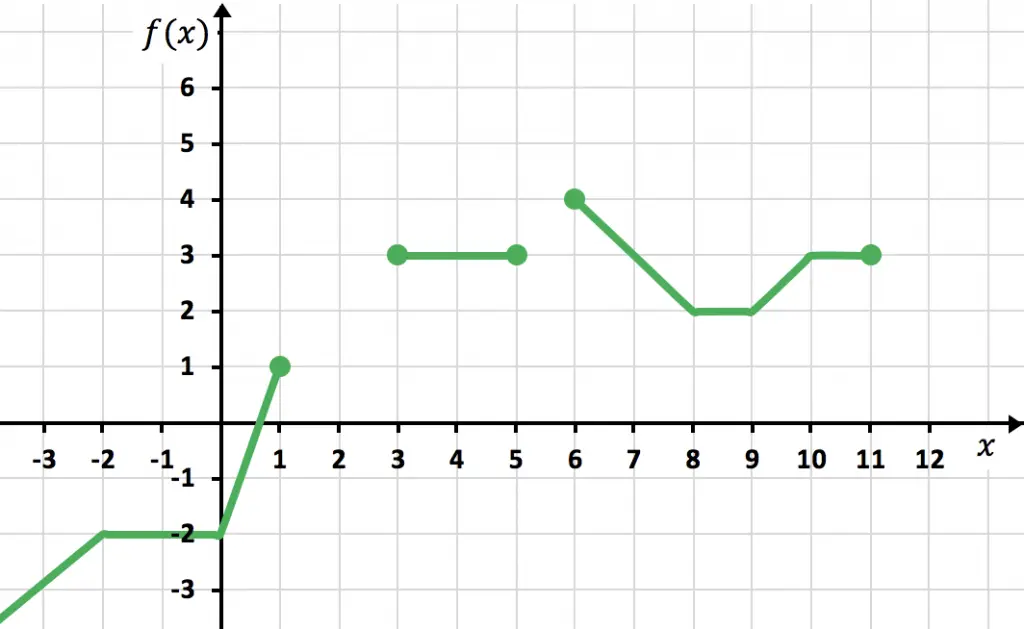
Para hallar el dominio nos fijamos en el eje horizontal:
- La función viene desde
y existe hasta
- Luego la función también existe entre
y
- Y finalmente la función también existe en el tramo entre
y
Por lo tanto el dominio de la función es:
Debemos poner un corchete en todos los intervalos porque todos son puntos cerrados. Con excepción del -∞ y el +∞, que siempre van con paréntesis.
Por otro lado, para encontrar el recorrido nos fijamos en el eje vertical:
- La función viene desde
y llega hasta
- Después la función también existe entre
y
- Pero nunca existe entre
y
ni nunca es más grande que
Por lo tanto el recorrido de la función es:
Igual que antes, debemos poner corchete en todos los intervalos porque todos son puntos cerrados. Y los infinitos siempre van con paréntesis.
Ejercicio 2
Encuentra el dominio y el recorrido de la siguiente función gráficamente:
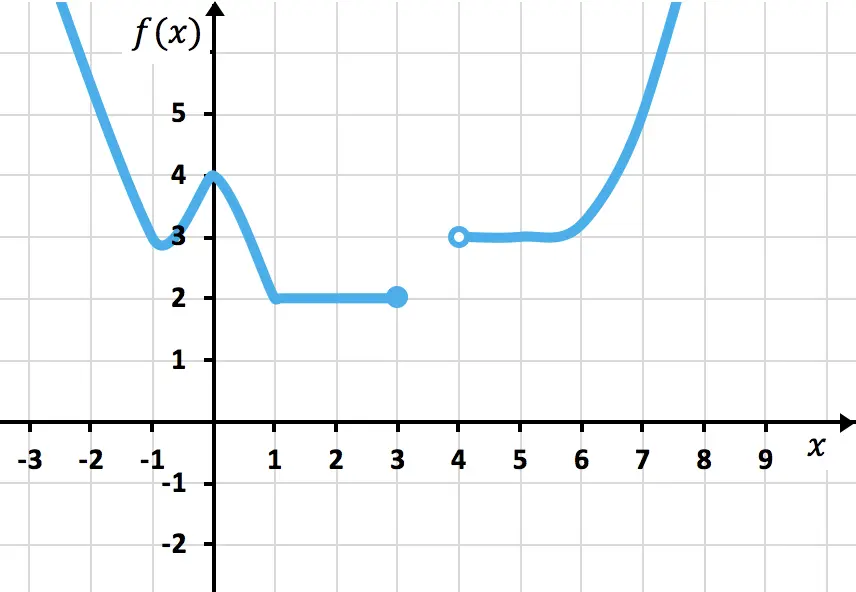
Para hallar el dominio de la función nos tenemos que centrar en el eje X:
- La función viene desde
y existe hasta
- Luego la función también existe entre
(no incluido) y
Ya que no vemos el final de la función y, por tanto, se va al infinito.
De manera que el dominio de la función es:
Recuerda que se debe poner corchete en los puntos cerrados y paréntesis en los puntos abiertos.
Por otra parte, para hallar el recorrido nos tenemos que fijar en el eje Y:
- La función existe desde
y hasta
- Pero nunca existe por debajo de
De modo que el recorrido de la función es:
Como el 2 también se incluye, ponemos un corchete. A parte, -∞ y +∞ siempre van con paréntesis.
Ejercicio 3
Calcula el dominio y el recorrido de la función representada en el siguiente gráfico:
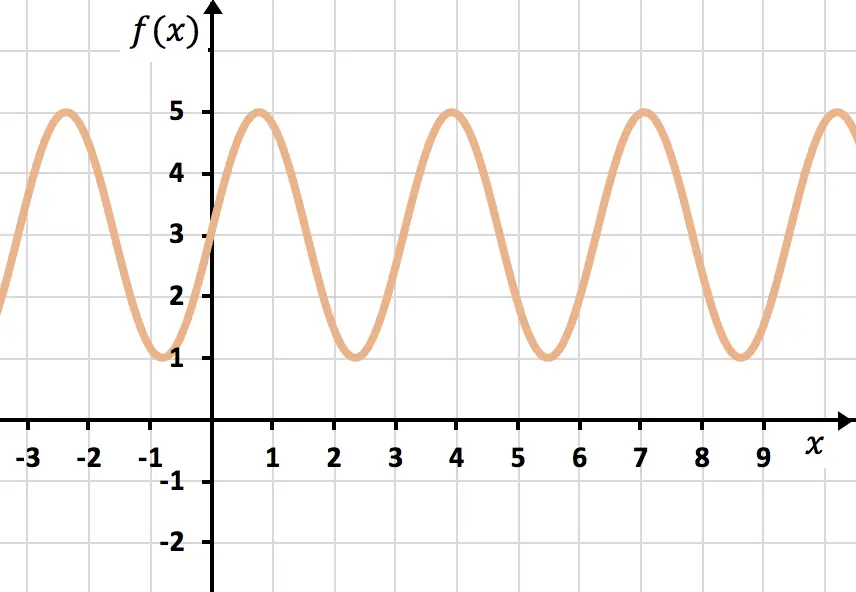
Para encontrar el dominio de la función nos fijamos en el eje horizontal:
- La función viene desde
y va hasta
sin ninguna interrupción.
Por lo tanto el dominio de la función es desde -∞ hasta +∞, es decir, son todos los números reales:
Para encontrar el recorrido de la función nos fijamos en el eje vertical:
- La función únicamente existe desde
hasta
Por lo que el recorrido de la función es:
Debemos poner corchete en el 1 y el 5 porque también se incluyen. Es decir, existe y
Ejercicio 4
Calcula el dominio de la siguiente función polinómica no lineal:
Se trata de una función polinómica, de manera que su dominio son todos los números reales:
Ejercicio 5
Calcula el dominio de la siguiente función con una fracción:
Se rata de una función racional, por tanto, el dominio son todos los números menos el punto en el que se anula el denominador, ya que entonces la función daría ∞.
Así que igualamos a cero todo el denominador para ver qué número no pertenece al dominio:
Resolvemos la ecuación:
De modo que el dominio de la función son todos los números excepto el -2:
Ejercicio 6
Saca el dominio de la siguiente función con una raíz:
Es un función radical de índice par, por tanto, la función existirá siempre que el contenido de la raíz sea igual o más grande que 0 (porque no existe la raíz cuadrada de un número negativo):
Resolvemos la inecuación:
La solución son todos los números más grandes o iguales que -3. Así que el dominio de la función es:
Como la inecuación tiene el signo ≥, que contiene el signo igual, debemos poner un corchete al lado del -3. A parte, -∞ y +∞ siempre van con paréntesis.
Ejercicio 7
Halla el dominio de la siguiente función radical:
Se trata de una función radical de índice par, por tanto, la función existirá siempre que el contenido de la raíz sea igual o más grande que 0 (porque no existe la raíz cuadrada de un número negativo):
Es una inecuación de segundo grado, ya que tiene un término al cuadrado. Por tanto, primero tenemos que resolverla como si fuera una ecuación de segundo grado normal, y luego mirar qué tramos cumplen la inecuación:
Ahora representamos el 2 y el -1 en la recta:

Y sustituimos un número de cada tramo en la inecuación, para ver qué tramos cumplen la inecuación y, en consecuencia, son solución:
✅
❌
Recuerda que cuanto más negativo es un número, más pequeño es.
✅
Por tanto la solución son los tramos de los lados:

Y el intervalo que les corresponde es:
Fíjate que debemos poner corchetes porque los puntos son cerrados, ya que la inecuación tiene el signo ≥. A parte, -∞ y +∞ siempre van con paréntesis.
De modo que el dominio de la función es:
Ejercicio 8
Calcula el dominio de la siguiente función exponencial:
Se trata de una función exponencial, de modo que el dominio son todos los números reales:
Ejercicio 9
Define el dominio de la siguiente función compuesta por varios tipos de funciones:
Se trata de una función exponencial, así que el dominio deberían ser todos los números reales. Pero en el exponente hay una función radical de índice par , por lo tanto, la función existirá siempre que el contenido de la raíz sea igual o más grande que 0:
Resolvemos la inecuación:
La solución son todos los números más grandes o iguales que 0. Así que el dominio de la función es:
Como la inecuación tiene el signo ≥, que contiene el signo igual, debemos poner un corchete. A parte, -∞ y +∞ siempre van con paréntesis.
Ejercicio 10
Calcula el dominio de la siguiente función con un logaritmo:
Se trata de una función logarítmica, y no existe ni el logaritmo de un número negativo ni el logaritmo de 0. Por tanto, la función existirá siempre que el argumento del logaritmo sea positivo (más grande que cero):
Resolvemos la inecuación:
La solución son todos los números más grandes que 2. Así que el dominio de la función es:
Como la inecuación tiene el signo >, que no contiene el signo igual, debemos poner un paréntesis al lado del 2. A parte, -∞ y +∞ siempre van con paréntesis.
Ejercicio 11
Calcula el dominio de la siguiente función:
En el denominador de la fracción tenemos una función radical de índice par, por tanto, la función existirá siempre que el contenido de la raíz sea igual o mayor que cero:
Pero, además, la raíz está en el denominador de la fracción. Y el denominador de una fracción nunca puede ser 0. Por tanto, la función solo existirá si el contenido de la raíz es estrictamente más grande que 0:
Ahora resolvemos la inecuación:
Recuerda que cuando en una inecuación cambiamos de lado un número negativo multiplicando o dividiendo, también tenemos que girar el signo de la inecuación.
El resultado son todos los números más pequeños que -4. Así que el dominio de la función es:
Como la inecuación tiene el signo <, que no contiene el signo igual, debemos poner un paréntesis al lado del -4. A parte, -∞ y +∞ siempre van con paréntesis.

Excelente, me sirvió mucho para repasar.
Saludos.
¡Genial Jerson! ¡Me alegro!
Buen dia, me gusta mucho la forma en la que esta escrita su pagina web, se entiende perfectamente y además se puede practicar. Creo que usted también es el propietario de la página de Matrices y Determinantes y geometría analitica info, otras dos páginas que también me sirvieron para mi aprendizaje, ¿Podría porfavor enviarme los enlaces a sus otras páginas para consultar mis temas de estudio?
No se si tenga una página donde explique integrales y otra para espacios vectoriales que es lo que necesito por el momento, me interesaría mucho verlas si se explican los temas como en esta pagina, gracias!
Hola David,
¡Muchísimas gracias por tu comentario! Por lo que respecta a la explicación sobre las integrales y los espacios vectoriales, actualmente ninguna página web habla sobre ello, pero en un futuro está previsto ampliar funciones.xyz y geometriaanalitica.info con estos temarios.
Por otro lado, te dejos los enlaces de todas las páginas webs de matemáticas que pedías, aunque algunas aún están en proceso de construcción:
Muy buena página! Tenía los conocimientos mezclados ya que un «profesor de particular» me daba la didáctica sin explicación y fundamentos. ¡¡¡Felicitaciones por el trabajo, molestia e inversión de su tiempo para que la página sea clara y concisa!!!
¡¡Muchísimas gracias Ivan!! ¡¡Se agradecen comentarios tan positivos!!
Quedé muy fascinado con esta página, tengo un certamen próximo de cálculo diferencial que le tengo terror porque si no apruebo, repruebo el ramo :c, el contenido aquí me aclara muchas dudas que mi profesor me deja y no me explica tan claramente, incluso es más fácil entender aquí. Agradecido con todo el esfuerzo de esto. De casualidad, tendrá o conocerá una página similar sobre química??. Bendiciones.
¡Muchísimas gracias Nicolás! ¡Intentamos hacerlo lo mejor posible para que los concepts sean fáciles de entender!
Aún no hemos hecho ningún sitio web relacionado con química, pero nos lo apuntamos para un futuro.
Por si te interesa, te dejo varios sitios webs nuestros de diferentes materias: