Derivada del arcoseno

En este post te explicamos cómo derivar el arcoseno de una función. Encontrarás ejemplos de derivadas del arcoseno de funciones e incluso podrás practicar con ejercicios resueltos paso a paso. Por último, también podrás ver la demostración de la fórmula de la derivada del arcoseno.

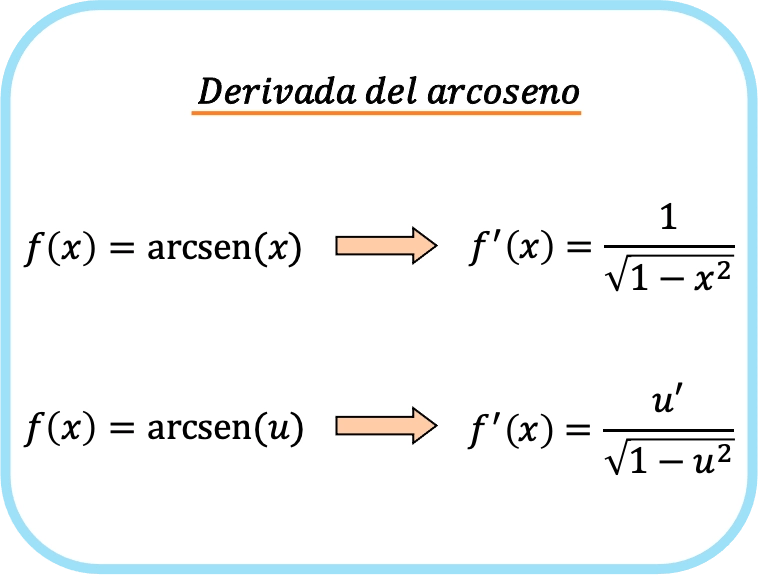
¿Cuál es la derivada del arcoseno?

La derivada del arcoseno de x es uno partido por la raíz cuadrada de uno menos x al cuadrado.

f(x)=\text{arcsen}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{1-x^2}}

Por lo tanto, la derivada del arcoseno de una función es igual al cociente de la derivada de esa función dividido entre la raíz cuadrada de uno menos la función al cuadrado.

f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}

Lógicamente, la segunda fórmula se obtiene de aplicar la regla de la cadena a la primera fórmula.

derivada del arcoseno

Recuerda que el arcoseno es la función inversa del seno, por eso también se llama seno inverso.

Ejemplos de la derivada del arcoseno

Después de ver cuál es la fórmula de la derivada del arcoseno, pasamos a explicar varios ejemplos de este tipo de derivadas trigonométricas. De esta manera te será más fácil entender cómo se deriva el arcoseno de una función.

Ejemplo 1: Derivada del arcoseno de 2x

f(x)=\text{arcsen}(2x)

Para hallar la derivada de la función arcoseno, debemos usar su fórmula correspondiente:

f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}

Así pues, la derivada de 2x es 2, por lo que la derivada del arcoseno de 2x es 2 divido por la raíz de uno menos 2x al cuadrado:

f(x)=\text{arcsen}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\sqrt{1-(2x)^2}}=\cfrac{2}{\sqrt{1-4x^2}}

Ejemplo 2: Derivada del arcoseno de x al cuadrado

f(x)=\text{arcsen}(x^2)

Utilizamos la fórmula de la derivada del arcoseno para hacer su derivación:

f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}

La función x2 es de segundo grado, así que su derivada es 2x. Por lo tanto, la derivada del arcoseno de x elevada a la 2 es:

f(x)=\text{arcsen}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=\cfrac{2x}{\sqrt{1-x^4}}

Ejemplo 3: Derivada del arcoseno de ex

f(x)=\text{arcsen}(e^x)

La función de este ejemplo es una función compuesta, de modo que debemos aplicar la regla de la cadena para resolver la derivada:

f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}

La derivada de ex es ella misma, así que la derivada de toda la función es:

f(x)=\text{arcsen}(e^x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{e^x}{\sqrt{1-\left(e^x\right)^2}}=\cfrac{e^x}{\sqrt{1-e^{2x}}}

Ejercicios resueltos de la derivada del arcoseno

Deriva las siguientes funciones arcoseno:

\text{A) }f(x)=\text{arcsen}(6x)

\text{B) }f(x)=\text{arcsen}(x^2-4x)

\text{C) }f(x)=\text{arcsen}\left(3x^4-6x^3+9+e^{x^2}\right)

\text{D) }f(x)=\text{arcsen}\left(\log_5(3x)\right)

\text{E) }f(x)=\text{arcsen}\left(\sqrt{4x}\right)

\text{A) }f'(x)=\cfrac{6}{\sqrt{1-(6x)^2}}=\cfrac{6}{\sqrt{1-36x^2}}

\text{B) }f'(x)=\cfrac{2x-4}{\sqrt{1-(x^2-4x)^2}}

\text{C) }f'(x)=\cfrac{12x^3-18x^2+2x\cdot e^{x^2}}{\sqrt{1-(3x^4-6x^3+9+e^{x^2})^2}}

\text{D) }f'(x)=\cfrac{1}{\sqrt{1-\left(\log_5(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 5}=\cfrac{1}{x\cdot \ln 5\cdot \sqrt{1-\left(\log_5(3x)\right)^2}}

\begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}

 

Demostración de la fórmula de la derivada del arcoseno

A continuación, procedemos a demostrar matemáticamente la fórmula de la derivada del arcoseno.

y=\text{arcsen}(x)

Primero de todo, transformamos el arcoseno en seno:

x=\text{sen}(y)

Ahora derivamos en los dos lados de la ecuación:

1=\text{cos}(y)\cdot y'

Despejamos y’:

y'=\cfrac{1}{\text{cos}(y)}

Luego, aplicamos la identidad trigonométrica fundamental:

\text{sen}^2(y)+\text{cos}^2(y)=1 \ \longrightarrow \ \text{cos}(y)=\sqrt{1-\text{sen}^2(y)}

y'=\cfrac{1}{\sqrt{1-\text{sen}^2(y)}}

Y, como arriba hemos deducido que x era equivalente al seno de y, la igualdad queda:

y'=\cfrac{1}{\sqrt{1-x^2}}

Como puedes ver, aplicando este procedimiento hemos conseguido la fórmula de la derivada de la función arcoseno, por lo que queda demostrado que se cumple la fórmula.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *