▷ Derivada de un producto (fórmula y ejercicios resueltos)

En este post te explicamos cómo derivar el producto de dos funciones (fórmula). Además, podrás ver varios ejemplos de derivadas de productos de funciones e, incluso, practicar con ejercicios resueltos de derivadas de multiplicaciones.

Índice

Fórmula de la derivada de un producto

La derivada de un producto de dos funciones diferentes es igual al producto de la derivada de la primera función por la segunda función sin derivar más el producto de la primera función sin derivar por la derivada de la segunda función.

Es decir, sean f(x) y g(x) dos funciones distintas, la fórmula de la derivada de la multiplicación entre las dos funciones es la siguiente:

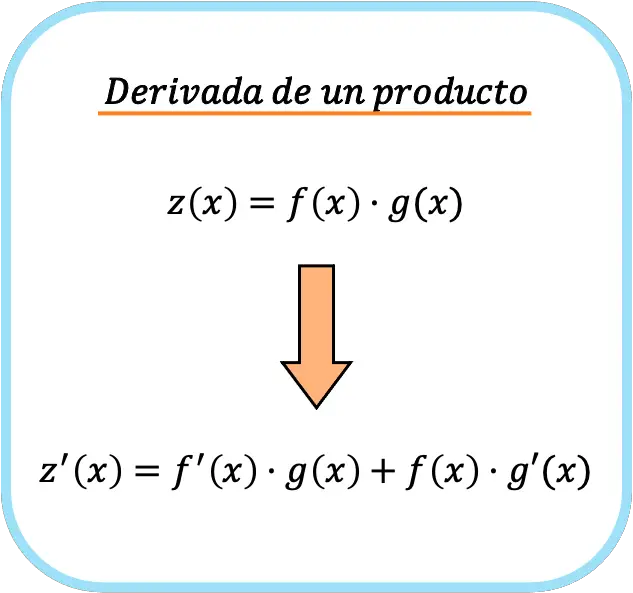
De manera que al aplicar la regla de la derivada de un producto pasamos de una sola multiplicación a tener dos productos distintos.

Ejemplos de la derivada de un producto

Una vez sabemos cuál es la fórmula de la derivada de un producto (o multiplicación), vamos a resolver varios ejemplos de este tipo de derivadas. Así te resultará mucho más fácil entender cómo se deriva un producto de dos funciones.

Ejemplo 1

En este ejemplo resolveremos la derivada de dos funciones potenciales multiplicándose:

$f(x)=5x^2\cdot (x^3+4x-6)$

Como hemos visto en el apartado anterior, la fórmula de la derivada de una multiplicación es:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Por lo tanto, primero tenemos que calcular la derivada de cada función por separado:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

Y una vez conocemos la derivada de cada función, podemos aplicar la fórmula de la derivada del producto de dos funciones. Es decir, multiplicamos la derivada del primer factor por el segundo factor sin derivar y luego sumamos el producto del primer factor sin derivar por la derivada del segundo factor:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

Finalmente, hacemos las operaciones para simplificar el resultado obtenido:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

Ejemplo 2

En este caso derivaremos el producto de una constante por una función:

$f(x)=7\cdot (x^2+3x)$

La regla de la derivada de un producto es la siguiente:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Entonces, derivamos cada función que forma parte del producto por separado:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

Y luego aplicamos la regla de la derivada de una multiplicación:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

Fíjate que a derivada de una constante siempre es cero, por lo tanto, se puede deducir que la derivada de la multiplicación de una constante por una función es igual al producto de la constante por la derivada de la función.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

Ejemplo 3

Vamos a resolver el producto entre una función exponencial y un logaritmo natural:

$f(x)=4^{3x}\cdot \ln(x^2)$

La fórmula de la derivada de una multiplicación de dos funciones es:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Así que primero debemos hacer la derivada de cada función que forma el producto por separado, que son las siguientes:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

De modo que el producto de funciones derivado es:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

Ejercicios resueltos de la derivada de un producto

Deriva los siguientes productos de funciones:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

Ver solución

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

Derivada de un producto de tres funciones

A continuación, te dejamos con la fórmula de la derivada de la multiplicación de 3 funciones, ya que es muy parecida a la de 2 funciones y puede resultarte útil en algunos casos.

La derivada de una producto de tres funciones es igual al producto de la derivada de la primera función por las otras dos funciones, más el producto de la derivada de la segunda función por las otras dos funciones, más el producto de la derivada de la tercera función por las otras dos funciones.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

Por ejemplo, si queremos derivar la siguiente multiplicación de tres funciones distintas:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

Para resolver la derivada tenemos que aplicar la regla de la derivada del producto de tres funciones, por tanto:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

Demostración de la fórmula de la derivada de un producto

Finalmente, demostraremos la fórmula de la derivada de una multiplicación. No es necesario que la memorices, pero siempre es bueno entender de dónde vienen las fórmulas. 🙂

Partiendo de la definición matemática de la derivada:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sea la función z el producto de dos funciones distintas:

$z(x)=f(x)\cdot g(x)$

Entonces la derivada de z, según la definición, será:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Como sabemos, si añadimos un término sumando y restando, este no afecta al resultado mientras los dos sean el mismo término. De modo que podemos hacer el siguiente paso:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

Ahora utilizamos las propiedades de los límites para separar el límite anterior en dos límites diferentes:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

Extraemos factor común en el numerador de las dos fracciones:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

Por otro lado, conocemos el resultado del siguiente límite:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

Por tanto, podemos simplificar los límites:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Finalmente, si nos fijamos en los dos límites restantes, cada uno corresponde a la definición de la derivada de una función. De modo que la igualdad se puede simplificar:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

O equivalentemente:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

6 comentarios en “Derivada de un producto (o multiplicación)”

Jesús Fuentes
29/08/2021 a las 16:01

Muy buen contenido.

Responder
1. Funciones
  31/08/2021 a las 08:27
  
  ¡Muchas gracias Jesús! 😉
Hugo
25/08/2022 a las 04:02

Excelente y resumido contenido.

Responder
1. Funciones
  25/08/2022 a las 20:46
  
  ¡Gracias Hugo!
DULCE MARIA
15/11/2022 a las 16:22

¿CÓMO CITO ESTE CONTENIDO?

Responder
1. Funciones
  16/11/2022 a las 14:41
  
  Buenas,
  
  Para citar este artículo simplemente debes mencionar el título, añadir la URL del artículo y decir la fecha en la que consultaste el artículo.

Fórmula de la derivada de un producto

Ejemplos de la derivada de un producto

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejercicios resueltos de la derivada de un producto

Derivada de un producto de tres funciones

Demostración de la fórmula de la derivada de un producto

6 comentarios en “Derivada de un producto (o multiplicación)”

Deja un comentario Cancelar respuesta