En este post te explicamos cómo derivar la secante hiperbólica de una función. Encontrarás la fórmula de la derivada de la secante hiperbólica y varios ejemplos resueltos de este tipo de derivada.
Índice
Fórmula de la derivada de la secante hiperbólica
La derivada de la secante hiperbólica de x es igual a menos el producto de la secante hiperbólica de x por la tangente hiperbólica de x.
Por lo tanto, la derivada de la secante hiperbólica de un función es menos el producto de la secante hiperbólica de la función por la tangente hiperbólica de la función por la derivada de dicha función.
En definitiva, la fórmula de la derivada de la función secante hiperbólica es la siguiente:
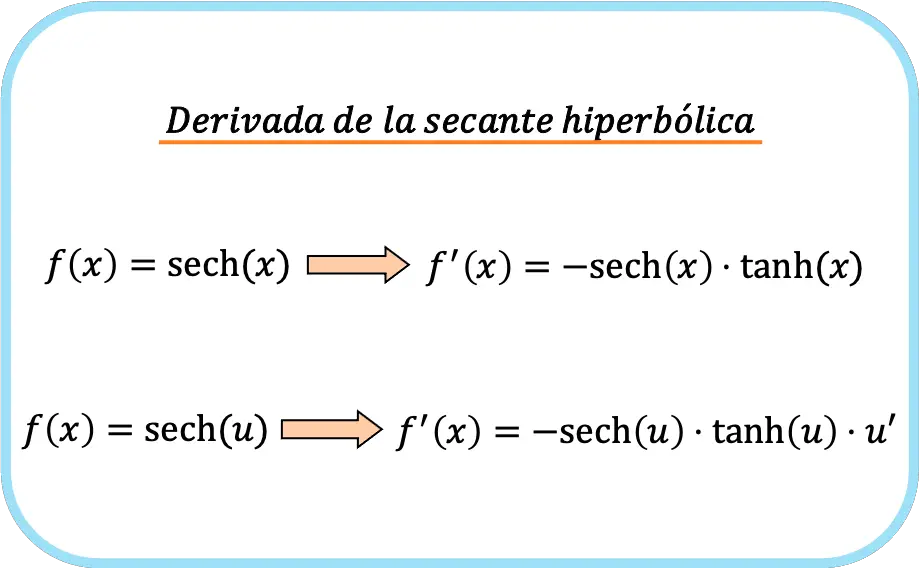
Ten en cuenta que las dos expresiones en realidad pertenecen a una única fórmula. La única diferencia es que en la segunda fórmula se aplica la regla de la cadena.
Ejemplos de la derivada de la secante hiperbólica
Ahora que ya sabemos cuál es la fórmula de la derivada de la secante hiperbólica, vamos a ver varios ejercicios resueltos de este tipo de derivada trigonométrica.
Ejemplo 1
En este ejemplo tenemos una función diferente de x en el argumento de la secante hiperbólica, así que para derivarla tenemos que usar la fórmula con la regla de la cadena.
Como la función 2x es lineal, su derivada es 2. Por lo tanto, para hallar la derivada simplemente debemos sustituir en la fórmula la u por 2x y la u’ por 2:
Ejemplo 2
La función de este ejercicio es compuesta, pues la secante hiperbólica tiene otra función en su argumento. De modo que debemos usar la fórmula de la secante hiperbólica con la regla de la cadena para hacer su derivación:
La derivada de x elevada a 2 da 2x, por lo tanto, la derivada de la secante hiperbólica de x al cuadrado es:
