▷ Asíntota oblicua de una función (ejercicios resueltos)

En este post te explicamos qué son las asíntotas oblicuas de una función. Encontrarás cuándo una función tiene asíntota oblicua y cómo se calcula. Y, además, podrás ver ejemplos de asíntotas oblicuas y practicar con ejercicios resueltos paso a paso.

Índice

¿Qué es una asíntota oblicua?

La asíntota oblicua de una función es una recta inclinada a la cual su gráfica se va aproximando indefinidamente sin llegar nunca a cruzarla. Por lo tanto, todas las asíntota oblicuas son rectas de ecuación y=mx+n.

La pendiente y la ordenada en el origen de una asíntota oblicua se calculan utilizando las siguientes fórmulas:

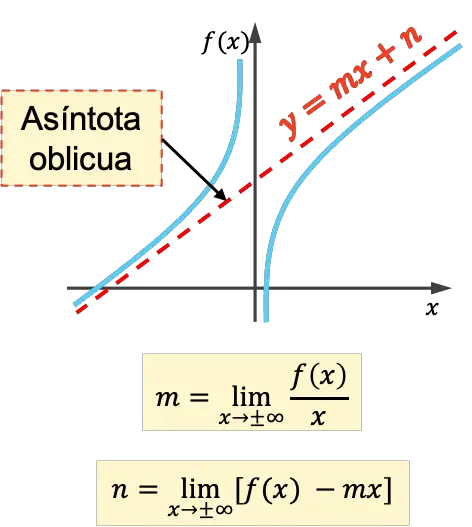
Cómo calcular la asíntota oblicua de una función

Para calcular la asíntota oblicua de una función, se deben hacer los siguientes pasos:

Calcular el límite en el infinito de la función partido por x.
Si el límite anterior da un número real diferente de cero, significa que la función tiene una asíntota oblicua. Y, además, la pendiente de dicha asíntota oblicua será el valor obtenido en el límite.

$\displaystyle m = \lim_{x \to \pm\infty}\frac{f(x)}{x}$

En tal caso, solo falta calcular la ordenada en el origen de la asíntota oblicua resolviendo el siguiente límite:

$\displaystyle n = \lim_{x \to \pm\infty} [f(x)-mx]$

Nota: los límites se deben calcular en el más y en el menos infinito, pero normalmente dan el mismo resultado y por eso se simplifica poniendo ±∞. Pero si los límites en el más y en el menos infinito fuesen distintos, deberíamos calcular por separado la asíntota oblicua por la izquierda y la asíntota oblicua por la derecha.

Ejemplo de asíntota oblicua

A continuación vamos a sacar la asíntota oblicua de la siguiente función racional para que veas un ejemplo de cómo se hace:

$f(x)=\cfrac{x^2+1}{x}$

Las asíntotas oblicuas son del tipo $y=mx+n.$ Así que primero calculamos la pendiente de la recta $m$ con su fórmula correspondiente:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}$

Para resolver este límite debemos aplicar las propiedades de las fracciones:

$\cfrac{\cfrac{a}{b}}{\cfrac{c}{d}}=\cfrac{a\cdot d}{b\cdot c}$

$\displaystyle m= \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+1}{x}}{x}=\lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2}$

Y ahora calculamos el límite:

$\displaystyle m = \lim_{x \to \pm\infty} \cfrac{x^2+1}{x^2} = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = \bm{1}$

En este caso el resultado de la indeterminación infinito entre infinito es la división de los coeficientes de las x de mayor grado, ya que el numerador y el denominador son del mismo orden.

El límite anterior da un número real distinto de cero, por lo tanto, la función tiene una asíntota oblicua. Ahora vamos a calcular la ordenada al origen $n$ de la asíntota usando su fórmula correspondiente:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right]$

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]$

Intentamos calcular el límite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Pero obtenemos la indeterminación infinito menos infinito. De modo que debemos reducir los términos a común denominador. Para ello, multiplicamos y dividimos la x por el denominador de la fracción:

$\displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]$

Ahora que los dos términos tienen el mismo denominador, los podemos juntar:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}$

Operamos en el numerador:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}$

Y, finalmente, resolvemos el límite:

$\displaystyle n = \lim_{x \to \pm\infty} \cfrac{\phantom{2}1\phantom{2}}{x}= \cfrac{1}{\pm\infty} = \bm{0}$

De modo que n=0. Por tanto, la asíntota oblicua es una función lineal:

$y = mx+n$

$y = 1x+0$

$\bm{y=x}$

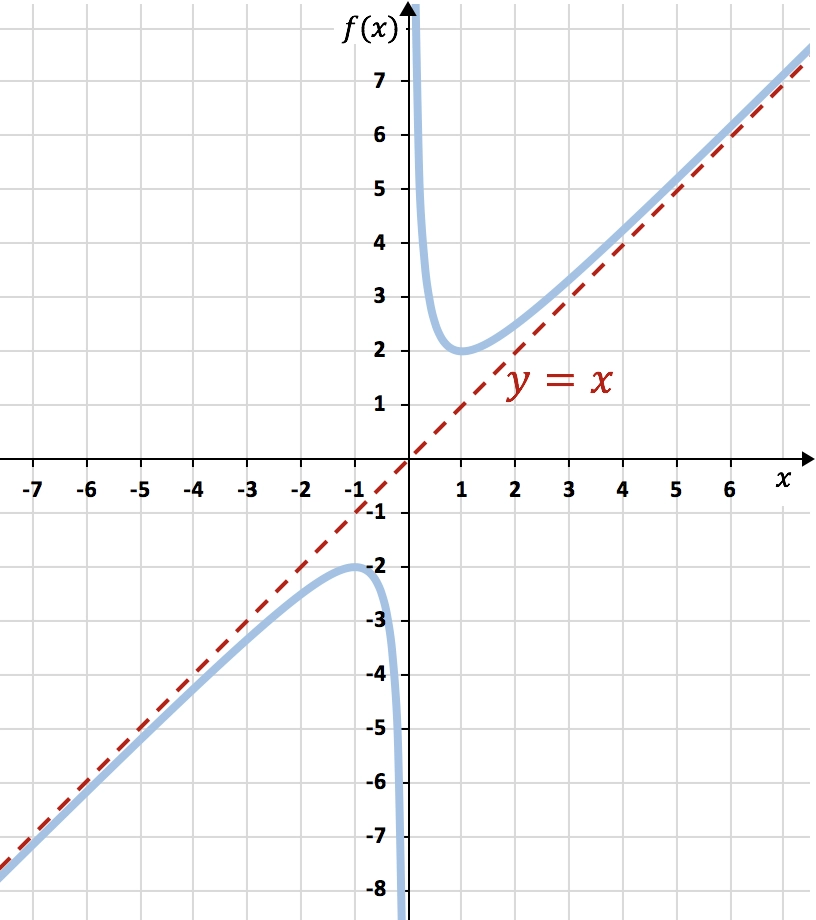
En el gráfico de abajo está representada la función estudiada. Como puedes ver, la función se va acercando mucho a la recta y=x pero nunca la llega a tocar porque es una asíntota oblicua:

Ejercicios resueltos de asíntotas oblicuas

Ejercicio 1

Halla la asíntota oblicua de la siguiente función racional:

$\displaystyle f(x)= \frac{x^2+2x+3}{x+1}$

Ver solución

Las asíntotas oblicuas son de la forma $y=mx+n$ , por lo que debemos calcular los parámetros m y n. Primero calculamos m aplicando su fórmula:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{x^2+2x+3}{x+1}}{x}$

Simplificamos la fracción aplicando las propiedades de las fracciones:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{(x+1)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}$

Y resolvemos el límite:

$\displaystyle m =\lim_{x \to \pm\infty} \frac{x^2+2x+3}{x^2+x}= \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Por tanto, m=1. Ahora hacemos el cálculo de la ordenada en el origen de la asíntota oblicua aplicando su fórmula:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-1x\right]$

Intentamos calcular el límite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right]= \bm{+\infty - \infty}$

Pero obtenemos la forma indeterminada infinito menos infinito. Por tanto, tenemos que reducir los términos a común denominador y luego juntarlos:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}$

Y, por último, resolvemos el límite:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{x+3}{x+1} = \frac{\infty}{\infty} = \frac{1}{1} = \bm{1}$

En definitiva, la asíntota oblicua de la función es:

$y = mx+n$

$y = 1x + 1$

$\bm{y = x + 1}$

Ejercicio 2

Encuentra todas las asíntotas oblicuas de la siguiente función racional:

$\displaystyle f(x)=\frac{2x^2-5}{x+3}$

Ver solución

En primer lugar, usamos la fórmula de la pendiente de la asíntota oblicua:

$\displaystyle m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \cfrac{\cfrac{2x^2-5}{x+3}}{x}$

Simplificamos la fracción aplicando las propiedades de las fracciones:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{(x+3)\cdot x}$

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}$

Y determinamos el límite:

$\displaystyle m =\lim_{x \to \pm\infty}\frac{2x^2-5}{x^2+3x}= \frac{+\infty}{+\infty} = \frac{2}{1} = \bm{2}$

El límite da un número real diferente de cero, así que se trata de una función racional con asíntota oblicua cuya pendiente es 2.

Ahora calculamos la ordenada al origen aplicando su fórmula correspondiente:

$\displaystyle n = \lim_{x \to \pm\infty} \left[f(x)-mx\right] = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]$

Intentamos calcular el límite:

$\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]= \bm{+\infty - \infty}$

Pero obtenemos la indeterminación diferencia de infinitos. Por tanto, reducimos los términos a común denominador y luego operamos:

$\begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}$

Y, por último, resolvemos el límite:

$\displaystyle n =\lim_{x \to \pm\infty} \frac{-6x-5}{x+3}= \frac{\infty}{\infty}=\frac{-6}{1} = \bm{-6}$

En resumen, la asíntota oblicua de la función fraccionaria es:

$y = mx+n$

$\bm{y=2x-6}$

¿Qué es una asíntota oblicua?

Cómo calcular la asíntota oblicua de una función

Ejemplo de asíntota oblicua

Ejercicios resueltos de asíntotas oblicuas

Ejercicio 1

Ejercicio 2

Deja un comentario Cancelar respuesta