Aquí te explicamos cómo se resuelven los problemas de optimización de funciones por pasos. Además, podrás practicar con ejercicios resueltos de problemas de optimización.
Índice
¿Qué son los problemas de optimización?
Los problemas de optimización son problemas en los que hay que encontrar el máximo o el mínimo de una función. Por ejemplo, un problema de optimización sería calcular el máximo de una función que define los beneficios de una empresa.
Cómo resolver los problemas de optimización
Pasos para resolver los problemas de optimización de funciones:
- Plantear la función que se debe optimizar.
- Derivar la función a optimizar.
- Buscar los puntos críticos de la función a optimizar. Para ello, se deber igualar la derivada de la función a cero y resolver la ecuación resultante.
- Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Ejemplo de problema de optimización
Vista la teoría sobre los problemas de optimización, vamos a resolver un problema de este tipo paso a paso para que veas cómo se hacen.
- De todos los triángulos rectángulos cuyos catetos suman 10 cm, calcula las dimensiones del que tenga el área máxima.
Para resolver el problema, llamaremos a un cateto del triángulo x, y al otro cateto y:

Paso 1: Plantear la función a optimizar.
Queremos que el área del triángulo sea máxima, y la fórmula del área de un triángulo es:
En nuestro caso, la base del triángulo es x y su altura y. Por tanto:
Ya tenemos la función a optimizar, pero esta depende de dos variables cuando solo puede depender de una. Sin embargo, el enunciado nos dice que los dos catetos tienen que sumar 10 cm. Por tanto:
Despejamos y de esta ecuación:
Y sustituimos la expresión en la función:
Ahora ya tenemos la función a optimizar planteada y solo depende de una variable, por lo que podemos pasar al siguiente paso.
Paso 2: Calcular la derivada de la función a optimizar.
Se trata de una función racional, por tanto, aplicamos la fórmula de la derivada de una división para derivarla:
Paso 3: Buscar los puntos críticos.
Para buscar los puntos críticos de la función, tenemos que igualar la derivada a cero y resolver la ecuación resultante:
El 4 está dividiendo a todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Para estudiar la monotonía de la función, representamos en la recta el punto crítico encontrado:
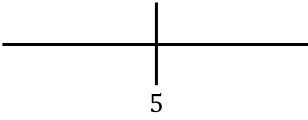
Y ahora evaluamos el signo de la derivada en cada intervalo para saber si la función crece o decrece. Para ello, cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
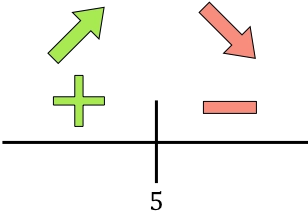
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por lo tanto, los intervalos de crecimiento y decrecimiento de la función son:
Crecimiento:
Decrecimiento:
En x=5 la función pasa de ser creciente a ser decreciente, así que x=5 es un máximo relativo de la función a optimizar.
Por tanto, x=5 es el valor del cateto del triángulo que hace el área máxima. Solamente nos queda calcular el valor del otro cateto:
En conclusión, los valores que maximizan el área del triángulo máxima son:
Problemas de optimización resueltos
Problema 1
Se administra una medicina a un enfermo y horas después la concentración en sangre del principio activo viene dada por la función
miligramos por mililitro. Determina el valor máximo de
e indica en qué momento se alcanza dicho valor.
Paso 1: Plantear la función a optimizar.
En este problema ya nos dan la función planteada, que es
Paso 2: Calcular la derivada de la función a optimizar.
La función está compuesta por el producto de 2 funciones. Por tanto, para calcular la derivada de la función tenemos que aplicar la regla de la derivada de un producto:
Paso 3: Buscar los puntos críticos.
Para buscar los puntos críticos de la función, resolvemos
Sacamos factor común para resolver la ecuación:
Para que la multiplicación valga 0, uno de los dos elementos de la multiplicación tiene que ser cero. Por lo tanto, igualamos cada factor a 0:
Un número elevado a otro número nunca puede dar 0, por tanto, no tiene solución.
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Para estudiar la monotonía de la función, representamos en la recta el punto crítico encontrado:
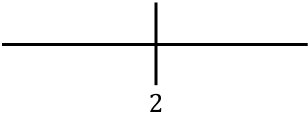
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
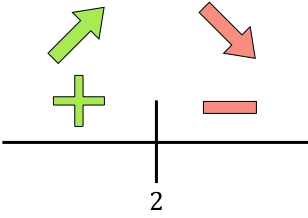
Si la derivada es positiva quiere decir que la función crece, por contra, si la derivada es negativa implica que la función decrece. De manera que los intervalos de crecimiento y decrecimiento de la función a optimizar son:
Crecimiento:
Decrecimiento:
La función pasa de ser creciente a ser decreciente en t=2, así que t=2 es un máximo de la función. Por tanto, la concentración máxima se alcanzará en t=2 horas.
Por último, sustituimos el valor en el que se produce el máximo en la función original, para hallar el valor de la concentración máxima:
Problema 2
Una tienda espera vender 40 patinetes eléctricos a un precio de 1000€ por patinete. Pero según un estudio de mercado, por cada 50€ de rebaja en el precio del patinete habrá un incremento de las ventas de 10 patinetes más vendidos.
Primero escribe la función de ingresos de la tienda en función del número de veces que se rebaje en 50€ el precio inicial de 1000€ del patinete. Luego, determina el precio del patinete para obtener el máximo de beneficios y los ingresos obtenidos con este precio.
Paso 1: Plantear la función a optimizar.
El enunciado del problema nos da una pista, ya que nos dice que la función tiene que depender del número de veces que se rebaje en 50€ el precio inicial. Por tanto, llamaremos x al número de veces que se rebaje 50€ el precio:
€
La función de ingresos será el número de patinetes vendidos multiplicado por el precio de cada patintete:
El número de patinetes vendidos será 40 más 10 patinetes por cada vez que rebaje el precio 50€. Por tanto:
El precio de cada patinete será 1000€ al principio, e irá disminuyendo 50€ cada vez que se rebaje el precio. Por tanto:
De manera que la función a optimizar del problema es:
Paso 2: Calcular la derivada de la función a optimizar.
Al ser una función polinómica, la derivada es más fácil de calcular:
Paso 3: Buscar los puntos críticos de la función.
Para buscar los puntos críticos de la función, resolvemos
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Para estudiar la monotonía de la función, representamos en la recta numérica el punto crítico calculado:
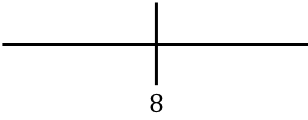
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
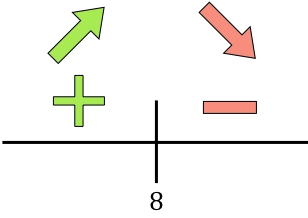
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:
Crecimiento:
Decrecimiento:
La función pasa de ser creciente a ser decreciente en x=8, así que x=8 es un máximo de la función. Por tanto, los ingresos máximos se producirán haciendo 8 veces la rebaja de 50€.
Ahora sustituimos el valor en el que se produce el máximo de ingresos en la función original, para hallar el valor de los ingresos máximos:
€
Y el precio de cada patinete después de hacer 8 veces la rebaja de 50€ será:
€
Problema 3
La función de costes (en miles de €) de una empresa se puede determinar mediante la siguiente expresión:
Donde representa los millares de unidades producidos de un determinado artículo.
Determina la cantidad que se debe producir para que el coste sea mínimo, cuál es ese coste y cuál sería el coste si no se produjese nada de ese artículo.
Paso 1: Plantear la función a optimizar.
El enunciado del problema ya nos proporciona la función a optimizar, que es
Paso 2: Calcular la derivada de la función a optimizar.
Paso 3: Buscar los puntos críticos.
Para buscar los puntos críticos de la función, resolvemos
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Representamos en la recta el punto crítico encontrado:
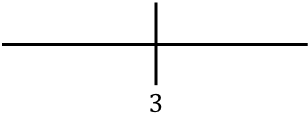
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
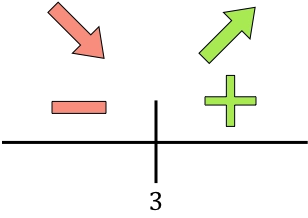
Si la derivada es mayor que cero, la función crece en ese intervalo. En cambio, si la derivada es menor que cero, la función decrece en ese intervalo. De forma que los intervalos de crecimiento y decrecimiento de la función son:
Crecimiento:
Decrecimiento:
La función pasa de ser decreciente a ser creciente en x=3, así que x=3 es un mínimo de la función. Por tanto, el coste mínimo se conseguirá produciendo 3 millares de unidades.
Ahora sustituimos el valor en el que se consigue el coste mínimo en la función original para hallar el valor del coste mínimo:
miles de €.
Por otro lado, nos preguntan cuál sería el coste si no se produjese nada, es decir cuando Por tanto, debemos calcular
miles de €.
Problema 4
Queremos construir un marco rectangular de madera que delimite un área de 2 m2. Sabemos que el precio de la madera es de 7,5 €/m para los lados horizontales y de 12,5 €/m para los lados verticales. Determina las dimensiones que debe tener el rectángulo para que el coste total del marco sea el mínimo posible y dicho coste mínimo.
Paso 1: Plantear la función a optimizar.
Para resolver el problema, llamaremos al lado horizontal x, y al lado vertical y:

Comprar un lado horizontal cuesta 7,5 €, y comprar un lado vertical 12,5 €. Además, por cada marco necesitamos dos lados horizontales y dos lados verticales. Por tanto, el coste del marco se puede determinar con la siguiente función:
Ya tenemos la función a optimizar. Pero esta depende de dos variables cuando solo puede depender de una. Sin embargo, el enunciado nos dice que el área del marco debe ser de 2 m2. Por tanto:
Despejamos la variable y:
Y sustituimos la expresión hallada en la función a optimizar:
Paso 2: Calcular la derivada de la función a optimizar.
Paso 3: Buscar los puntos críticos.
Para buscar los puntos críticos de la función, resolvemos
Multiplicamos en cruz para resolver la ecuación con fracciones:
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Representamos en la recta el punto crítico hallado para analizar la monotonía de la función:
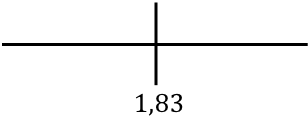
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
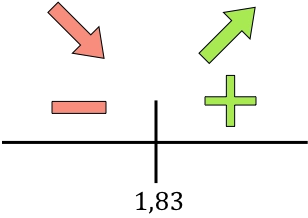
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:
Crecimiento:
Decrecimiento:
La función pasa de ser decreciente a ser creciente en x=1,83, así que x=1,83 es un mínimo de la función.
Por tanto, x=1,83 es el valor del lado horizontal que hace el coste mínimo. Ahora calculamos el valor del lado vertical:
De manera que los valores que hacen el coste del marco mínimo son:
Lado horizontal
Lado vertical
Y el coste mínimo que se consigue con estos valores es:
€
Problema 5
La puerta de una catedral está formada por un arco de media circunferencia que se apoya en dos columnas, tal y como muestra la siguiente figura:
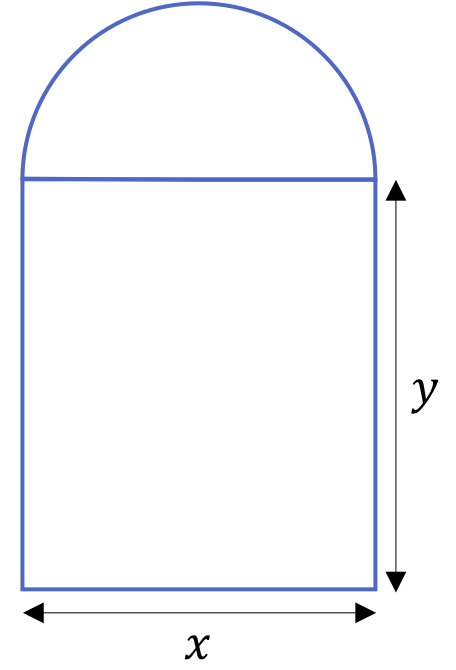
Si el perímetro de la puerta hace 20 m, determina las medidas e
que maximizan el área de toda la puerta.
Paso 1: Plantear la función a optimizar.
El área de una circunferencia se calcula con la fórmula De modo que el área de toda la puerta será el área del rectángulo más la mitad del área de la circunferencia:
Ya tenemos la función a optimizar. Pero esta depende de dos variables cuando solo puede depender de una.
Sin embargo, el enunciado nos dice que el perímetro de toda la puerta es de 20 m. El perímetro de una circunferencia se calcula con la fórmula Por tanto, el perímetro de toda la puerta será:
El perímetro tiene que ser 20 m. Así que igualamos la expresión anterior a 20 para hallar la relación entre e
Multiplicamos todos los términos por 2 para que eliminar las fracciones:
Despejamos
Y sustituimos la expresión hallada en la función a optimizar:
Paso 2: Calcular la derivada de la función a optimizar.
Paso 3: Buscar los puntos críticos.
Para buscar los puntos críticos de la función, resolvemos
Se trata de una ecuación con fracciones, así que multiplicamos cada término por el m.c.m. de los denominadores para eliminar las fracciones:
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Para estudiar la monotonía de la función, representamos en la recta el punto crítico encontrado:
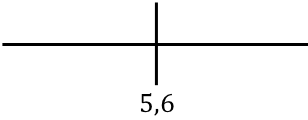
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
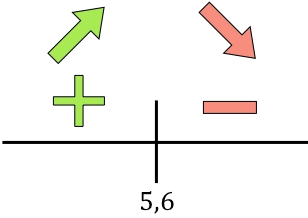
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:
Crecimiento:
Decrecimiento:
La función pasa de ser creciente a ser decreciente en x=5,6, así que x=5,6 es un máximo de la función.
Por tanto, es el valor que hace el área máxima. Ahora calculamos el valor de
De manera que los valores que hacen el área máxima son:
Problema 6
Se quiere construir un depósito en forma de cilindro que tenga una área de 54 cm2. Determina el radio de la base y la altura del cilindro para que el volumen sea máximo.
Paso 1: Plantear la función a optimizar.
El volumen de un cilindro se calcula con la siguiente fórmula:
El área de la base es una circunferencia, por lo que su fórmula es . De manera que la fórmula del volumen del cilindro queda:
Ya tenemos la función a optimizar. Pero esta depende de dos variables ( y
) cuando solo puede depender de una. Sin embargo, el enunciado nos dice que el área del cilindro debe ser de 54 cm2, así que aprovecharemos esta condición para hallar la relación entre
y
Para calcular el área de un cilindro tenemos que sumar su área lateral con las áreas de las dos bases:
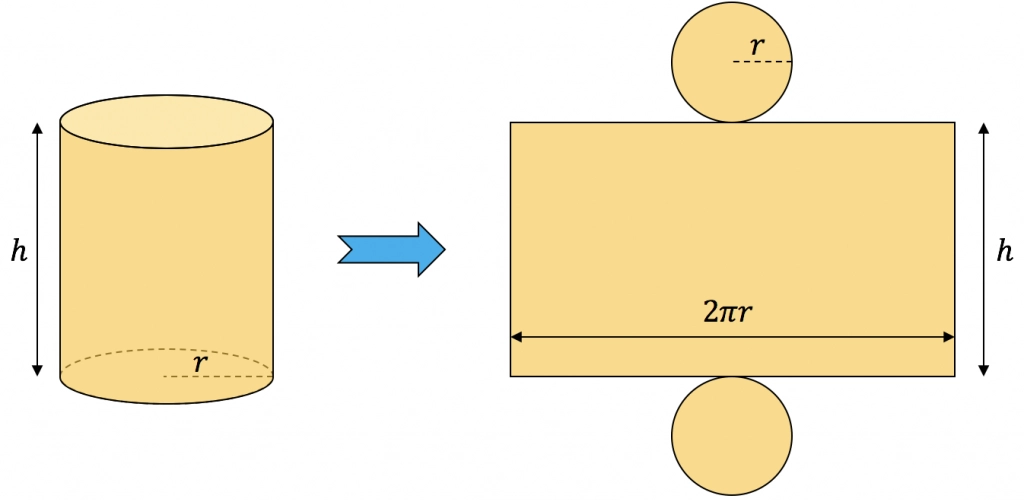
El área del cilindro tiene que ser de 54 cm2, así que igualamos la expresión anterior a 54 para obtener la relación entre y
Despejamos
Y sustituimos la expresión hallada en la función a optimizar:
Paso 2: Calcular la derivada de la función a optimizar.
Paso 3: Buscar los puntos críticos.
Para buscar los puntos críticos de la función, resolvemos
Paso 4: Estudiar la monotonía de la función y determinar el máximo o el mínimo de la función.
Para estudiar la monotonía de la función, representamos en la recta numérica el punto crítico encontrado:
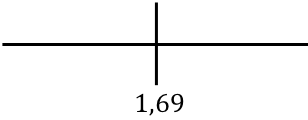
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca el punto crítico) y miramos qué signo tiene la derivada en ese punto:
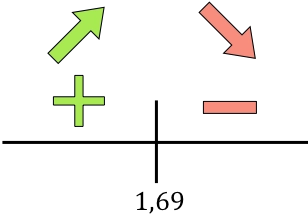
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:
Crecimiento:
Decrecimiento:
La función pasa de ser creciente a ser decreciente en r=1,69, así que r=1,69 cm es un máximo de la función.
Por tanto, r=1,69 es el valor del radio que hace el volumen máximo. Ahora calculamos la altura:
De manera que los valores que hacen el volumen máximo son:
Radio
Altura
